Gravity Train 3

Classical Mechanics Level 5

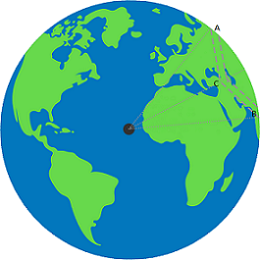
Two cities are situated at an angular distance of θ \theta with respect to Earth's center.

You are asked to find a broken-line tunnel A C B ‾ \overline{ACB} through Earth’s crust connecting the two cities such that it minimizes the time T T to commute between the cities when the train moves only under the influence of gravity.

What is this minimum T T ?

Details and Assumptions:

  • Assume Earth to be a sphere of uniform mass density with radius R R .
  • Ignore friction and collision.
2 R g sin ⁡ − 1 ( 1 − sin ⁡ θ 2 1 + sin ⁡ θ 2 ) 2\sqrt{\frac Rg}\sin^{-1}\left(\frac {1-\sin\frac\theta 2}{1+\sin\frac\theta 2}\right) 2 R g sin ⁡ − 1 ( 1 − cos ⁡ θ 2 1 + cos ⁡ θ 2 ) 2\sqrt{\frac Rg}\sin^{-1}\left(\frac {1-\cos\frac\theta 2}{1+\cos\frac\theta 2}\right) 2 R g cos ⁡ − 1 ( 1 − cos ⁡ θ 2 1 + cos ⁡ θ 2 ) 2\sqrt{\frac Rg}\cos^{-1}\left(\frac {1-\cos\frac\theta 2}{1+\cos\frac\theta 2}\right) 2 R g cos ⁡ − 1 ( 1 − sin ⁡ θ 2 1 + sin ⁡ θ 2 ) 2\sqrt{\frac Rg}\cos^{-1}\left(\frac {1-\sin\frac\theta 2}{1+\sin\frac\theta 2}\right)

Brian Lie by Brian Lie , 26, China

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

This not a solution, more an answer by inference. At θ = 0 , T = 0 \theta = 0, T = 0 . So, it can't be options B or C. At θ = 2 π \theta = 2\pi , option A gives bizarre results. Therefore, it's option D. :)

1 Helpful 1 Interesting 1 Brilliant 0 Confused

It should be at theta = 0 b is also ZERO And at theta equal to pi B holds good

raj abhinav - 1 year, 3 months ago

1 pending report

Vote up reports you agree with

×

Problem Loading...

Note Loading...

Set Loading...