GRE Question

Geometry Level 1

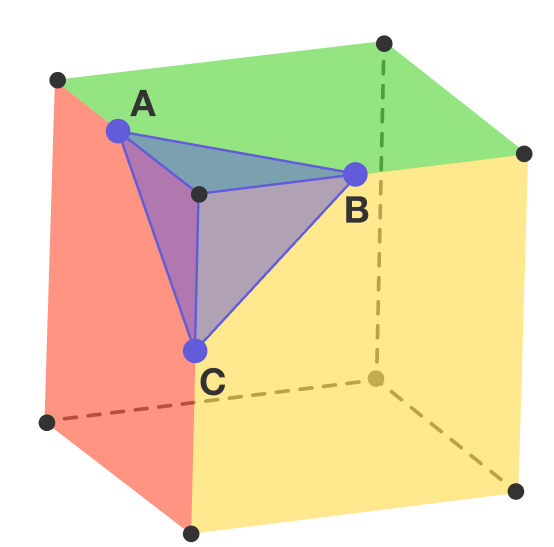
The volume of the cube shown above is 64. The vertices of triangle $ABC$ are the midpoints of the corresponding edges of the cube. What is the perimeter of triangle $ABC$ ?

6\sqrt{2}

12

6\sqrt{3}

6

12\sqrt{2}

1 solution

Sam Bealing
Jul 11, 2016

Relevant wiki: Pythagorean Theorem

The side length of the cube is $\sqrt[3]{64}=4$ so we can work out the side length of the triangle by Pythagoras:

$\sqrt{\left (\dfrac{4}{2} \right)^2+ \left (\dfrac{4}{2} \right)^2} =\sqrt{8}=2 \sqrt{2}$

By symmetry, all 3 sides of the triangle are the same so the perimeter is:

$3 \times 2 \sqrt{2}=\boxed{\boxed{6 \sqrt{2}}}$

100% correct. Thank you for the solution.

Hana Wehbi - 4 years, 11 months ago

GRE Question

1 solution

0 pending reports