Greatest integer sums

Relevant wiki: 2-dimensional Geometric Probability

If the fractional parts (portions after the decimal) add up to less than 1, the two will be equal, otherwise unequal. The probability is zero that they'd add to exactly 1, so that can be ignored. If the fractional parts are plotted on coordinate axes, the resulting unit square is divided by a diagonal line from $(0,1)$ to $(1,0)$ separating these two equal areas. The probability is $\boxed{\frac{1}{2}}$ .

Here, the only thing that matters are the decimals of x and y. There are two differents wways : either the sum of the decimals of x and y is >1 (=] 1; 2]), or the sum of the decimals of x and y is <1 (= [0; 1 [). These 2 cases therefore have the same probability : 1/2. This demonstration is by no means rigorous; I simply used my logic. This is my first.

I separated this into several different scenarios: The fractional part of x could either be less that 0.5 or greater than 0.5. The same is true for y. (Technically, it's possible that numbers with the fractional part exactly equal to 0.5, but this has probability zero as we are concerned with continuous numbers)

This leaves 4 equally likely scenarios:

1. Both x and y's fractional parts are less than 0.5, so the relation is satisfied. This will occur 1/4 of the time.
2. Both x and y's fractional parts are greater than 0.5, so the relation is NOT satisfied. This will occur 1/4 of the time.
3. x's fractional part is less than 0.5, and y's fractional part is greater than 0.5. Either the relation will be satisfied, or not, with equal probability giving a 1/8 chance for either.
4. x's fractional part is greater than 0.5, and y's fractional part is less than 0.5. Either the relation will be satisfied, or not, with equal probability giving a 1/8 chance for either.

Adding up the probabilities where it is satisfied gives 1/2.

I wrote (to my paper...) the same solution that is here already about twice, but here it is a little more precisely:

$\lfloor x+y \rfloor = \lfloor x \rfloor + \lfloor y \rfloor$ , when $\{x\} + \{y\}<1$ and $\lfloor x+y \rfloor = \lfloor x \rfloor + \lfloor y \rfloor +1$ , when $\{x\} + \{y\}\geq 1$ ( $\{ \cdot \}$ meaning the Fractional Part Function.)

That means, $P(\lfloor x+y \rfloor = \lfloor x \rfloor + \lfloor y \rfloor) = P(\{x\} + \{y\}<1) = P(u+v<1|u,v\in (0,1) )$

The last probability can be considered as graphical:

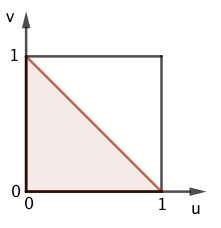
Shadowed part of the square being the satisfying area. It's area is clearly $\boxed{\frac12}$ .

Is this text understandable in any way?

I literally just guessed

The problem can be rewritten to separate the integer and decimal portions. X and Y are each the sum of a random integer A on some interval, and a random real α on the interval [0,1). I’ll use curly brackets for the floor function.

{X + Y} = {X} + {Y}

{A + α + B + β} = {A + α} + {B + β}

The integer portion can be separated from each floor function:

{A + α} = A + {α}

Rearranging:

A + B + {α + β} = A + B + {α} + {β}

α, β are less than one so {α} = {β} = 0. Subtract (A + B) from each side:

{α + β} = 0

Replace α+β=γ, where γ is a random number on the interval γ ∈ [0,2).

{γ} = 0

This statement is true when γ < 1, or equivalently, when γ∈[0,1). The interval [0,1) is half of the interval [0,2); therefore the likelihood of γ < 1 is 1/2.

It's the same as "What's the chance that 2 random numbers in the range 0-1 add up to more than 1?"

Suppose $\lfloor x \rfloor = n$ if $n \leq x < n+1$ and $\lfloor y \rfloor = m$ if $m \leq x < m+1$ for integers $n$ and $m$ by the definition of floor function.

Now, $x = n + 0.p$ and $y = m + 0.q$ where $p$ and $q$ are the decimal part of $x$ and $y$ respectively. Hence, $\lfloor x \rfloor = a$ and $\lfloor x \rfloor = b$

Moreover, $\lfloor x+y \rfloor = \lfloor n + m + 0.p + 0.q \rfloor$

Since $n$ and $m$ are integers, thus,

$\lfloor x+y \rfloor = \lfloor a \rfloor + \lfloor b \rfloor + \lfloor 0.p + 0.q \rfloor$

$\lfloor x+y \rfloor = \lfloor x \rfloor + \lfloor y \rfloor + \lfloor 0.p + 0.q \rfloor$

To make the equation true,

$0 \leq 0.p + 0.q < 1$

However, the values of $0.p + 0.q$ can be extended such that

$0 \leq 0.p + 0.q < 2$

Thus, the value of $0.p + 0.q$ must be in $[0,1)$ but it is allowable to $[0,2)$ . Therefore, half of the time the equation will be False . Thus, the probability is $\boxed{\frac{1}{2}}$

As many people have said the two sides of the equation are equal when {x} + {y} < 1. {x}-U[0,1] and {y}-U[0,1] so we have two identical continuous uniform distributions. Summing these two identical distrbutions will give us a symmetrical triangular distribution as long as the two distributions are independent which they are. (Think about what happens when you toss two dice and add up their two scores. Two uniform discrete distributions becomes triangular. The same follows for continuous distributions).Therefore {x}+{y}={z} where {z}-T(0,2). Since the probability density function makes a triangle with a line of symmetry about z=1 the probability of {x}+{y}<1 must be 1/2.

The sum of the integral parts of two numbers is equal to the integral part of their sum when the sum of their fractional parts do not sum over 1. The case that they sum exactly to 1 is of probability zero so we can be liberal with the signs.

So we want to calculate $P(X + Y < 1)$ given that $X, Y \sim U(0,1)$ . The CDF of the sum of two random variables is actually their convolutions, and the direct calculation is Thomas' soluton.

Another way to come out with the result is by symmetry. For every pair $x, y$ such that $x + y > 1$ , (w.l.o.g $x < y$ , being liberal with the signs here too), the pair $x, 1-y$ adds to a number less than one. Working from $x < y$ we have that $x - y < 0$ so $x + (1 - y) < 1$

Lets call $dec(x)$ the decimal part of x : $dec(x) = x - \lfloor x \rfloor$ As the equality required holds if the sum of decimal parts is less than 1, we have the equivalence : $P( \lfloor x+y \rfloor = \lfloor x \rfloor + \lfloor y \rfloor) = P( dec(x) + dec(y) < 1 )$

We can therefore reduce the problem to :
For two random positive real numbers $x$ and $y$ chosen uniformly and independently from the interval $(0,1)$ , determine the probability that $P( x + y < 1 )$ . This equals to : $P( x + y < 1 ) = P( y < 1 - x ) = \int_0^1 \int_0^{1-x} dy dx = \frac{1}{2}$

只看小数部分，就相当于在(0,2)没取两个数保证x+y＜1。用坐标系图像很容易得出½