Greedy algorithm
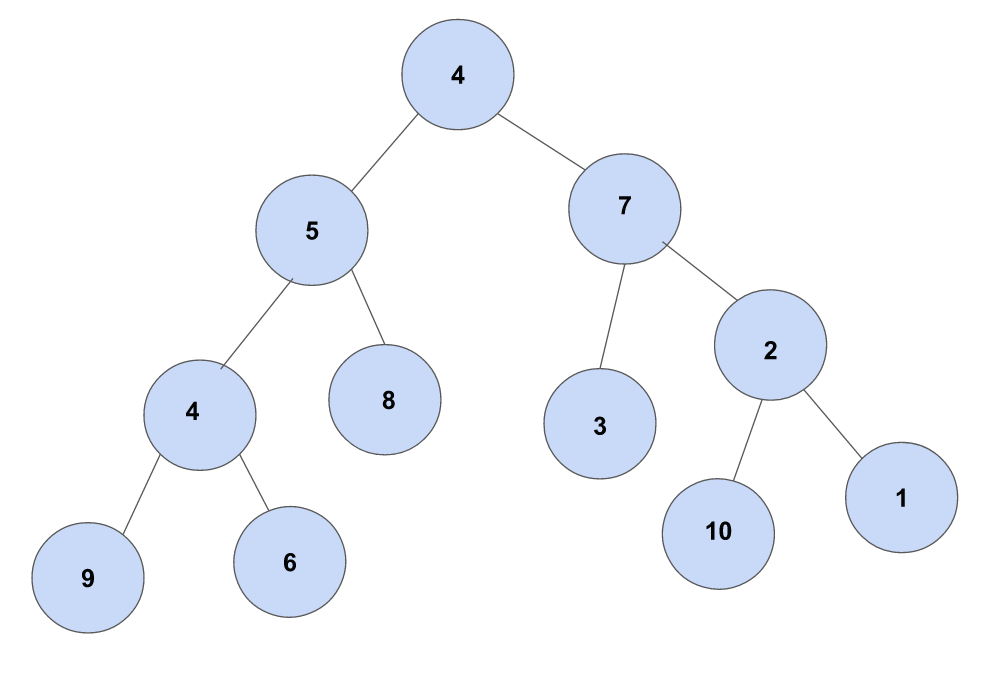
If there is a greedy algorithm that will traverse a graph, selecting the largest node value at each point until it reaches a leaf of the graph, what path will the greedy algorithm follow in the graph below?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
19 solutions
It doesnt work? I put 4-7-3 as my answer but it said i was incorrect.
the algorithm of this question is too greedy to give us the real answer , it seems
For sure lol
it should be 4, 7, 3
4 is the root node of the tree. Next we select 7 which is the largest number compared to 5. Lastly we select 3 which is greater than 2.
Greedy Algos 🐽 , are short-sighted so: it takes the bigger option every time... 4-7-3
It checks 5 or 7 -> goes to 7 -> then 3 or 2 -> Checks 3
As we travel from top to bottom, the first node is having the maximum values as 4, At second node as 7 > 5, 7 gets selected. At 3rd node as 3>2 3 gest selected.
4->7->3. The largest node at 2nd level is 7. Next we need to decide between 2 and 3 and 3 is larger.
I understood very well.
The root is 4 and as greedy, it takes large one which is 7 and when it reach next, it takes 3 means 4-7-3
Well, first of all remember that a leaf node is that node which don't have any subnode Rest, the problem is too easy ......
Choose greatest number at each step !
In greedy algorithm case, value from path the bigges will way to get the good solution. And then, From 4, becouse 5 < 7, so greedy will choice 7. And next steps, 2 < 3, the choice is 3. And this is the end of path.
The greedy algorithm takes the largest value at each step of the tree.
The greedy algorithm takes the biggest value at each step
As per given tree : Root 4 traverse towards child 7 due to it is great then 5. Same thing it is continued for next level where 3 is greater then 2. Also, the leaf 3 have no any further nodes belonging to it.
by considering traversing of above tree it is 4 > 7 > 3
Just select every maximu value in the adjacent node.
this is so sad
selecting maximum value always
The algorithm will select the largest node at each step. 4 is at the root of the tree so that is included in our solution immediately. Next, we select between 5 and 7. 7 is the larget number so we add that to our path. Next, we select between 3 and 2. 3 is the larger number, so we put that in our solution path, and we have reached a graph leaf so the algorithm stops.