Green area
The
P
,
Q
points are on the perimeter of the
A
B
C
D
rectangle as is shown on the figure below, such that
A
P
=
C
Q
=
3
and
B
P
=
D
Q
=
9
.
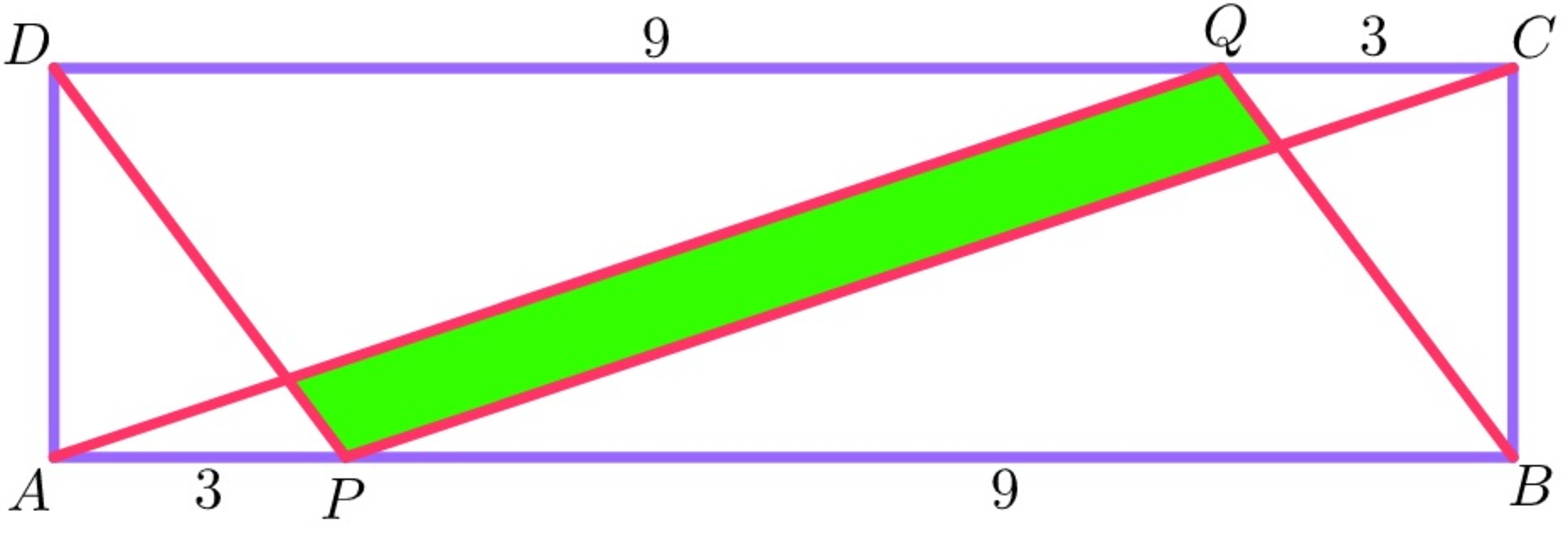
What is the area of the green quadrilateral, if the area of A B C D is 4 8 ?
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
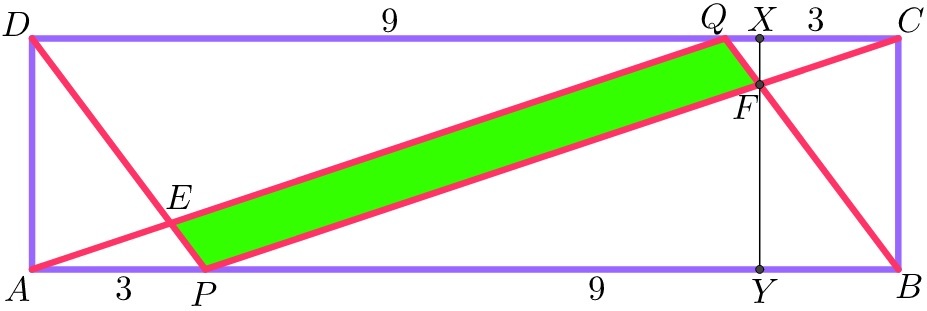
Since A P = C Q and A P ∣ ∣ C Q , the A P C Q quadrilateral is a parallelogram, [ A P C Q ] = A P ∗ B C = 3 ∗ 1 2 4 8 = 1 2 It is clear that △ P B F ∼ △ F C Q , and the similarity ratio is P B : Q C = 3 : 1 . From that F Y : F X = 3 : 1 (where F Y and F X are altitudes). Since X Y = B C = 4 , F X = 1 , [ Q C F ] = 2 3 ∗ 1 = 1 . 5 Since △ A P E ≅ △ C Q F , [ P F Q E ] = [ A P C Q ] − [ A P E ] − [ Q C F ] = [ A P C Q ] − 2 ∗ [ Q C F ] = 1 2 − 2 ∗ 1 . 5 = 9
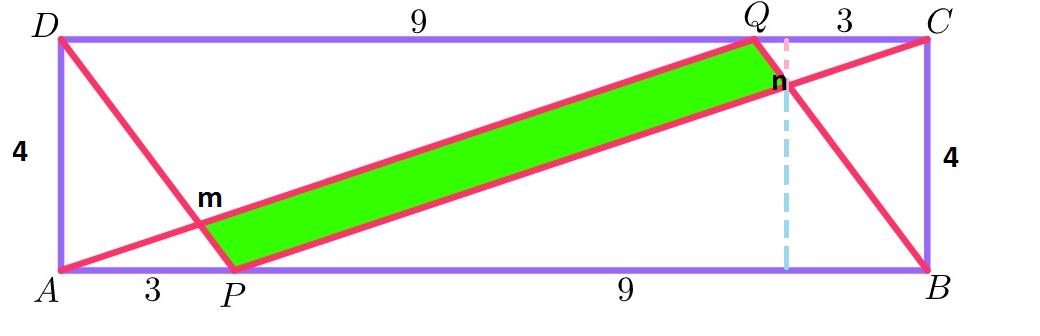
We know that C B is equal to 4 and that △ M A P is semelhant to △ P N B the ratio of similiarity is 3 1 also we know that their heights sum up to 4 now we can conclude △ P N B height is 3, so we have A B C D − ( 2 × △ P N B + 2 × △ D A P ) that is equal to 9
Use coordinate geometry.Let point A(0,0), and the intersection of line AQ and DP is R.Point D(0,4), P(3,0), and Q(9,4). So line DP has equation 4x+3y=12, and AQ: y=(4/9) x.The intersection point R(9/4, 1). The shaded area =2( [DPQ] – [DRQ]) = 2(18 – 9(3/2)) =9.
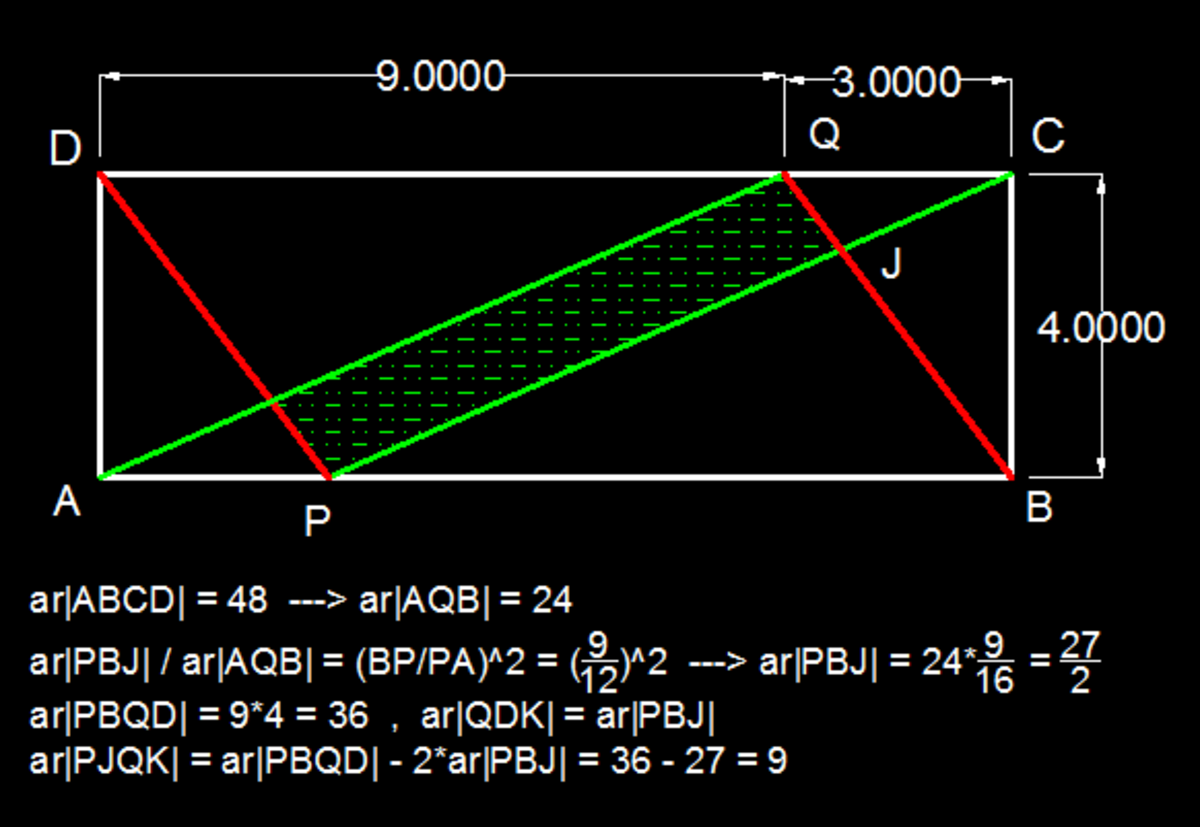
x = 9 0 − w = 5 3 . 1 3 0 1 0 2 3 5 ∘
tan z = 9 4 ⟹ z = 2 3 . 9 6 2 4 8 8 9 7 ∘
y = 1 8 0 − x − z = 1 0 2 . 9 0 7 4 0 8 7 ∘
By sine law ,
sin y 9 = sin x Q R ⟹ Q R = 7 . 3 8 6 6 4 3 3 5 2
Let A Y be the area of the yellow region, then A Y = 2 ( 2 1 ) ( 9 ) ( 7 . 3 8 6 6 4 3 3 5 2 ) ( sin z ) = 2 7
Let A B be the area of the blue region, then A B = 4 ( 3 ) = 1 2
Let A G be the area of the green region, then A G = 4 8 − 2 7 − 1 2 = 9
Note: In my computation I used the approximate values of the computed angles since they are not whole numbers. But It will arrive in the correct answer since it is accurate to 8 decimal places.