Green Light, Red Light
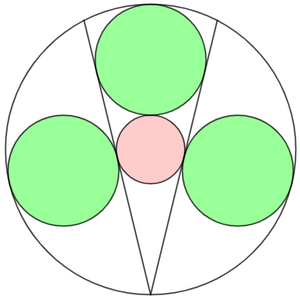
In the large circle, three green circles, each sharing one point of tangency with the outer circumference, and one red circle are arranged symmetrically, such that the red circle is tangent to each of the three circles. Each of the two green circles shares one point of tangency with the red circle at the midpoint of its respective chord. These two chords shares an intersection point at the circumference.
If the radius ratio of the green circle to the red circle is
b a ( c + d e )
where a , b , c , d , e are positive integers, g cd ( a , b ) = g cd ( c , d ) = 1 and e is square free, input a + b + c + d + e as your answer.
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
How did you arrive directly at the ratio, I got confused at the second last step, after proving the similarity
Log in to reply
cross-multiply 2 R + 3 G G = R + 2 G R to get G ( R + 2 G ) = R ( 2 R + 3 G ) .
distribute to get G R + 2 G 2 = 2 R 2 + 3 G R
add/subtract to get 2 G 2 − 2 G R − 2 R 2 = 0
divide everything by 2 to get G 2 − G R − R 2 = 0
use the quadratic formula to get G = 2 1 + 5 ⋅ R
oh yes :p, i got confused since in the solution in the rhs, the comma makes the 2G seem like 2G'
I just set red radius as 1 and solved
Let R be the radius of the red circle and G be the radius of the green circles, and label the diagram as follows:
Then O E = O B = O A + A B = R + 2 G , and C E = C O + O E = G + R + R + 2 G = 2 R + 3 G .
Since △ C D E ∼ △ O A E by AA similarity, C E C D = O E O A , or 2 R + 3 G G = R + 2 G R , which rearranges to R G = 2 1 ( 1 + 1 5 ) = ϕ , the golden ratio.
Therefore, a = 1 , b = 2 , c = 1 , d = 1 , e = 5 , and a + b + c + d + e = 1 0 .