Green's Theorem #1
Use Green's Theorem to evaluate where C is shown below.
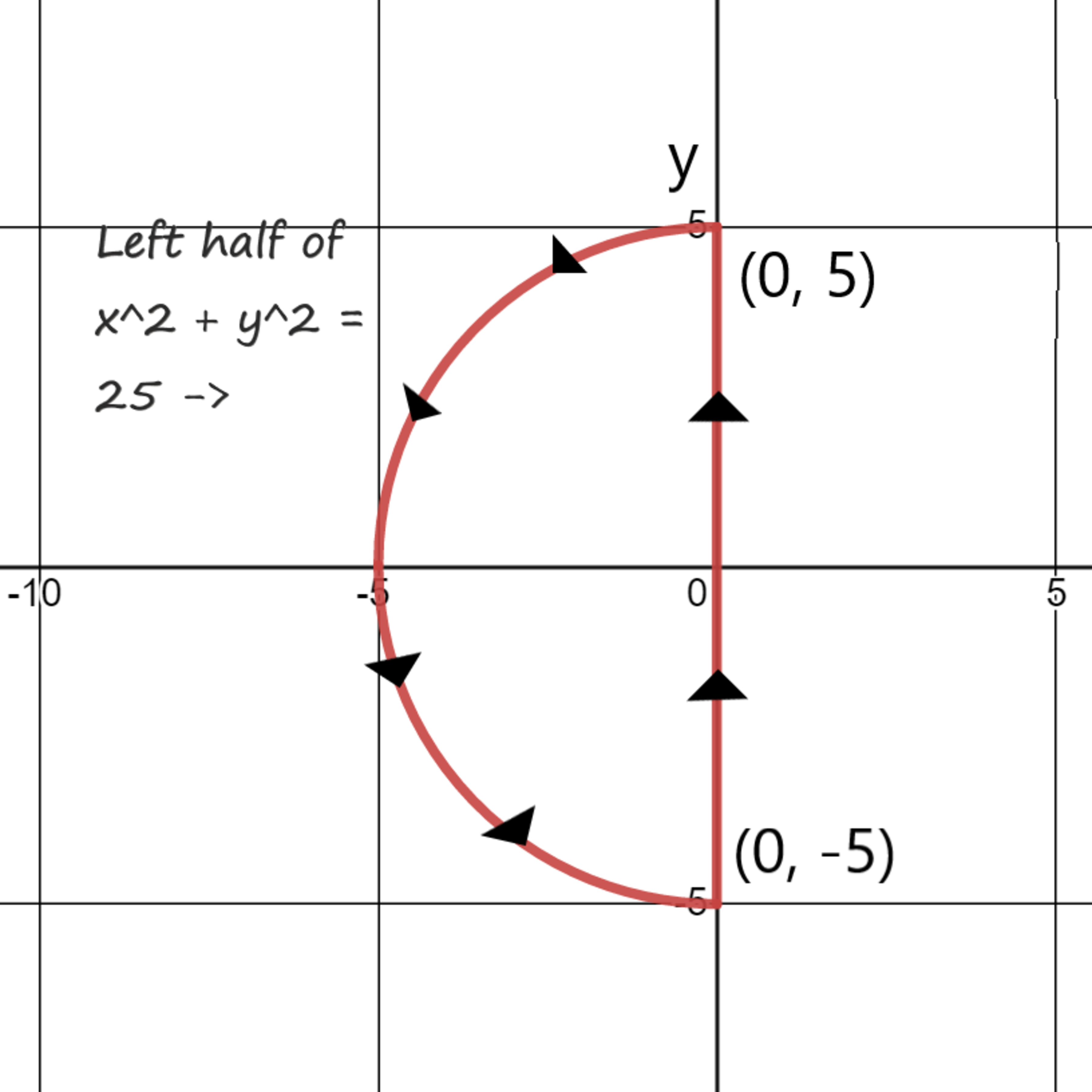
Provide your answer to three significant digits.
The answer is -78.8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First things first, if we walk along the path in the direction indicated in the diagram, then our left hand will be over the enclosed area. Therefore, this path has a positive orientation and we can use Green's Theorem to evaluate the integral.
Let's move on to the solution.
From the integral we have, P = y x 2 Q = − x 2 Remember that P is multiplied by x and Q is multiplied by y and don't forget to pay attention to signs.
Using Green's Theorem the line integral becomes, ∫ C y x 2 d x − x 2 d y = ∬ D − 2 x − x 2 d A D is the region enclosed by the curve.
Now, since D is just a half circle using polar coordinates is more suitable for this problem. Hence, the limits for D in polar coordinates are, 2 1 π ≤ t ≤ 2 3 π 0 ≤ r ≤ 5
Finally, all we need to do is evaluate the double integral, after converting to polar coordinates. The resulting steps are as follows:
∫ C y x 2 d x − x 2 d y = ∬ D − 2 x − x 2 d A = ∫ 2 1 π 2 3 π ∫ 5 0 r ( − 2 r cos θ − r 2 cos 2 θ ) d r d θ = ∫ 2 1 π 2 3 π ∫ 5 0 − 2 r 2 cos θ − 2 1 r 3 ( 1 + cos ( 2 θ ) ) d r d θ = ∫ 2 1 π 2 3 π ( − 3 2 r 3 cos θ − 8 1 r 4 ( 1 + cos ( 2 θ ) ) ) ∣ 0 5 d θ = ∫ 2 1 π 2 3 π − 3 2 5 0 cos θ − 8 6 2 5 ( 1 + cos ( 2 θ ) ) d θ = [ − 3 2 5 0 sin θ − 8 6 2 5 ( θ + 2 1 sin ( 2 θ ) ) ] ∣ 2 1 π 2 3 π = 3 5 0 0 − 8 6 2 5 π = − 7 8 . 7 7 0 3