Green's Theorem #2
Verify Green’s Theorem for where is shown below by using Green’s theorem to compute the line integral.
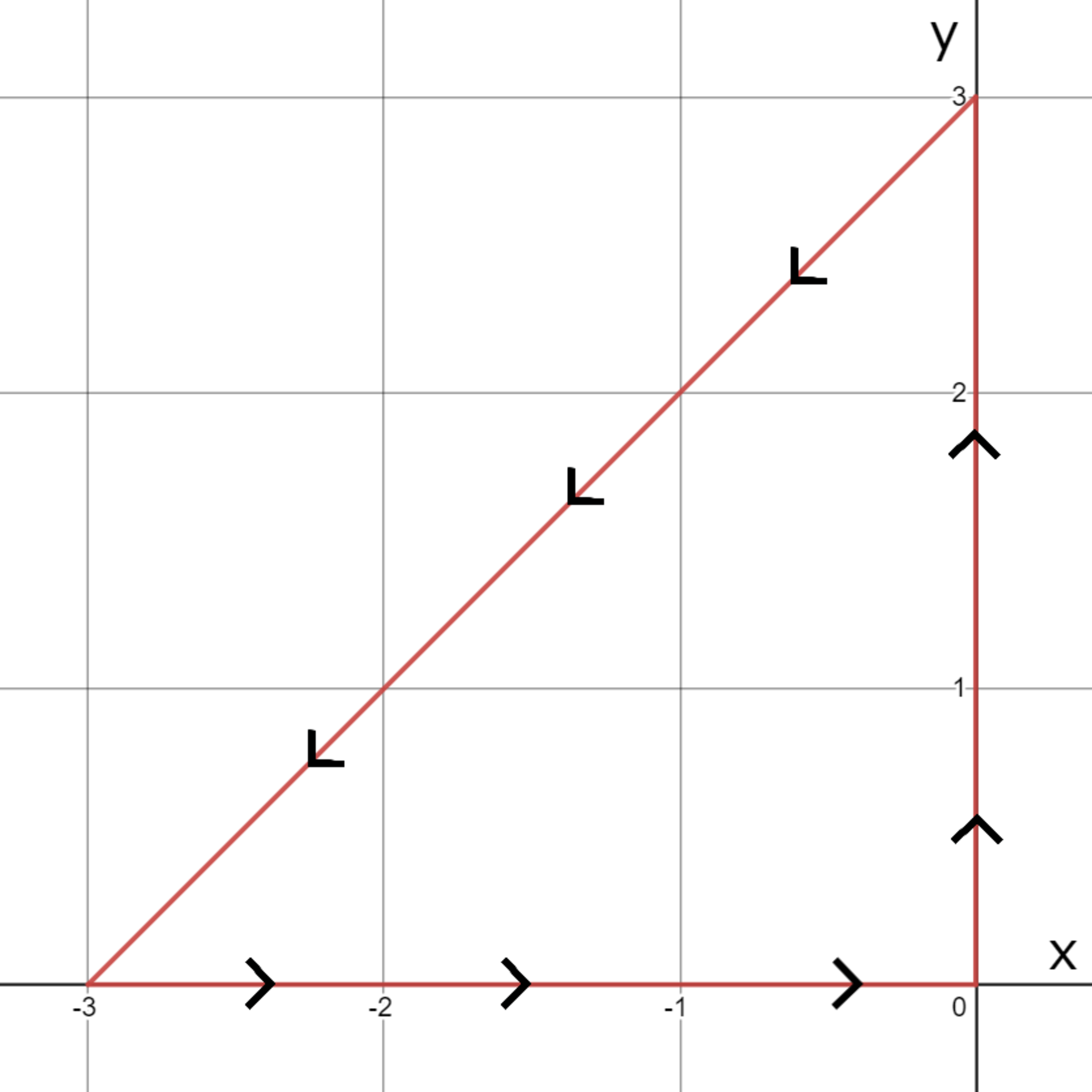
If this line integral is equal to where and are coprime positive integers, submit your answer as
The answer is 103.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Note that as the circle on the integral implies the curve is in the positive direction and so we can use Green’s Theorem on this integral.
From the integral we have, P = x y 2 + x 2 Q = 4 x − 1
Using Green’s Theorem the line integral becomes, ∮ C ( x y 2 + x 2 ) d x + ( 4 x − 1 ) d y = D ∬ 4 − ( 2 x y ) d A = D ∬ 4 − 2 x y d A
D is the region enclosed by the curve.
The equation of the line along the hypotenuse of the region is given by y = x + 3 . Once we have this equation the region is then very easy to get limits for. They are, − 3 ≤ x ≤ 0 0 ≤ y ≤ x + 3
Now all we need to do is evaluate the double integral. ∮ C ( x y 2 + x 2 ) d x + ( 4 x − 1 ) d y = D ∬ 4 − 2 x y d A = ∫ − 3 0 ∫ 0 x + 3 4 − 2 x y d y d x = ∫ − 3 0 ( 4 y − x y 2 ) ∣ ∣ 0 x + 3 d x = ∫ − 3 0 1 2 − 5 x − 6 x 2 − x 3 d x = ( 1 2 x − 2 5 x 2 − 2 x 3 − 4 1 x 4 ) ∣ ∣ ∣ ∣ − 3 0 = 4 9 9
Hence, the answer to this question is 9 9 + 4 = 1 0 3 .