Green's Theorem #3
Compute where is the counterclockwise-oriented boundary of upper-half unit disk
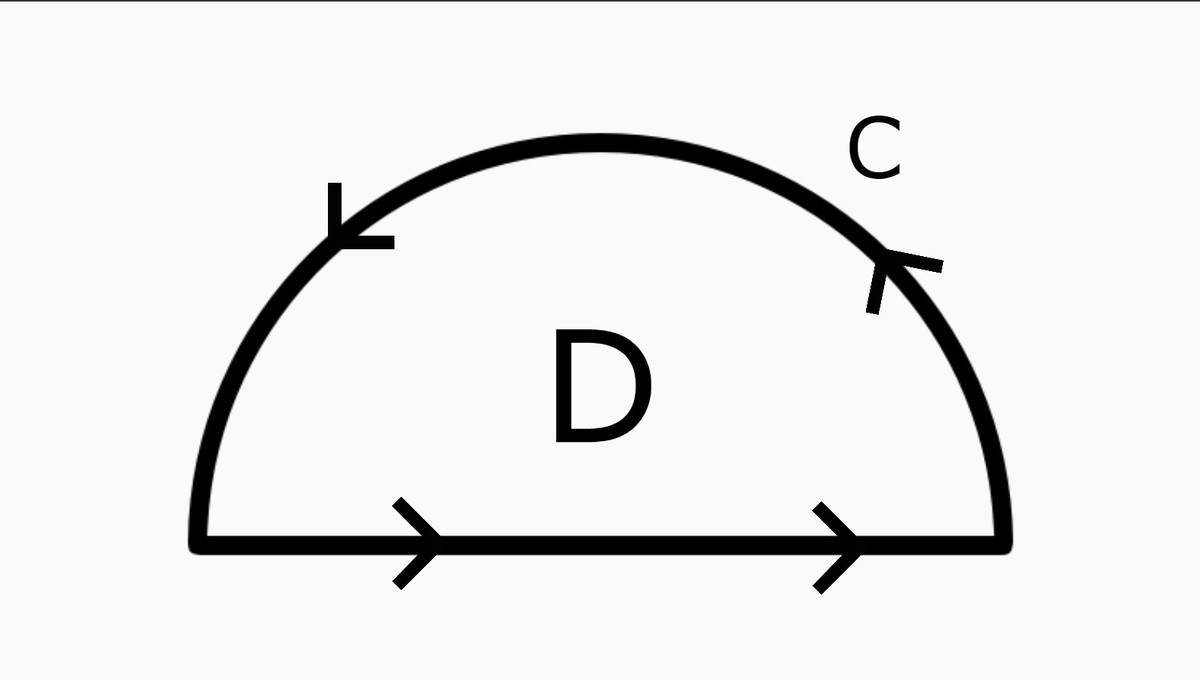
If this value is equal to where and are coprime positive integers, submit your answer as
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The vector field in the above integral is F ( x , y ) = ( y 2 , 3 x y ) . We can compute this integral using Green's theorem to convert the line integral into a double integral. The integrand of the double integral must be ∂ x ∂ F 2 − ∂ y ∂ F 1 = 3 y − 2 y = y .
Since the line integral was over the boundary of the half disk, the region of integration for the double integral is the half-disk D itself. (Since C was oriented counterclockwise, the orientation matches; otherwise, we would have had to multiple by negative one to get the correct sign.) The region D is described by − 1 ≤ x ≤ 1 , 0 ≤ y ≤ 1 − x 2 .
Therefore, by Green's Theorem, ∮ C y 2 d x + 3 x y d y = ∬ D ( ∂ x ∂ F 2 − ∂ y ∂ F 1 ) d A = ∬ D y d A = ∫ − 1 1 ∫ 0 1 − x 2 y d y d x = ∫ − 1 1 ( 2 y 2 ∣ ∣ ∣ ∣ y = 0 y = 1 − x 2 ) d x = ∫ − 1 1 2 1 − x 2 d x = 2 x − 6 x 3 ∣ ∣ ∣ ∣ − 1 1 = 3 2 .
Hence, the answer is 2 + 3 = 5 .