Grid of Sums

This is a very crude solution; I'll polish this up later.

Use brute force; there are only $9!$ combinations. The following code is pretty straightforward, although one-character names might be hard to follow.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

import itertools

neighbors = [(-1,-1), (-1,0), (-1,1), (0,-1), (0,1), (1,-1), (1,0), (1,1)]

def move(G, x, y):
    if G[x][y] != 0: return G[x][y]
    r, c = len(G), len(G[0])
    ans = 0
    for dx, dy in neighbors:
        if 0 <= x+dx < r and 0 <= y+dy < c: ans += G[x+dx][y+dy]
    if ans == 0: ans = 1
    return ans

def compute(r, c, P, print_grid=False):
    assert(list(sorted(P)) == list(range(r*c)))
    G = [[0]*c for _ in range(r)]
    for i in P:
        x, y = i//c, i%c
        ans = move(G, x, y)
        G[x][y] = ans
        if print_grid:
            print(x, y)
            for row in G: print(row)
    return ans

def solve(r, c):
    mx = 0
    perms = []
    for P in itertools.permutations(range(r*c)):
        ans = compute(r, c, P)
        if ans == mx: perms.append(P)
        if ans > mx:
            mx = ans
            perms = [P]
    return mx, perms

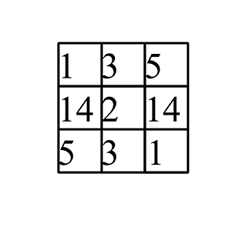
We have $mx = \boxed{57}$ . perms has all the permutations reaching the maximum; one of it is $(0,2,1,3,4,6,7,5,8)$ , which corresponds to A C B D E G H F I in the following:

The grid is

My perl code: (not all that elegant but it did the job... Its random, but it gets to 57 pretty quick! :) )

============================================================================

 for ($n =0; $n<1000000; $n++) {
    while ($a[1][1] * $a[1][2] * $a[1][3] * $a[2][1] * $a[2][2] * $a[2][3] * $a[3][1] * $a[3][2] * $a[3][3] == 0) {
            $x = 1+int(rand(3)); $y = 1+int(rand(3));
            if (! $a[$x][$y]) {
                    $a[$x][$y] = $a[$x-1][$y-1]  + $a[$x-1][$y] + $a[$x-1][$y+1] + $a[$x][$y+1] + $a[$x+1][$y+1] + $a[$x+1][$y] + $a[$x+1][$y-1] + $a[$x][$y-1];
                    $last = $a[$x][$y];
                    if ($a[$x][$y] == 0) {$a[$x][$y] = 1}
            }
    }
    if ($last > $max) {$max = $last}
    print "$max\n";
    ClearGrid();
}

sub ClearGrid() {for ($i=1;$i<4;$i++) {for ($j=1;$j<4;$j++) {$a[$i][$j] =0}}}

Similar to Ivan's solution, I used brute-force. Marking the squares from top-left by 1 and bottom-right by 9, we try all sequence of filling in the squares.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

#include <bits/stdc++.h>
using namespace std;

int max_num(int a[]) {

    int g[10]; memset(g,0,sizeof(g));
    for (int i = 0; i < 9; i++) {
        int cell = a[i];

        if      (cell == 1) g[cell] = g[2] + g[4] + g[5];
        else if (cell == 2) g[cell] = g[1] + g[3] + g[4] + g[5] + g[6];
        else if (cell == 3) g[cell] = g[2] + g[5] + g[6];
        else if (cell == 4) g[cell] = g[1] + g[2] + g[5] + g[7] + g[8];
        else if (cell == 5) g[cell] = g[1] + g[2] + g[3] + g[4] + g[6] + g[7] + g[8] + g[9];
        else if (cell == 6) g[cell] = g[2] + g[3] + g[5] + g[8] + g[9];
        else if (cell == 7) g[cell] = g[4] + g[5] + g[8];
        else if (cell == 8) g[cell] = g[4] + g[5] + g[6] + g[7] + g[9];
        else if (cell == 9) g[cell] = g[5] + g[6] + g[8];

        if (g[cell] == 0)
            g[cell] = 1;
    }

    return g[a[8]];
}

int a[] = {1,2,3,4,5,6,7,8,9};

int main() {

    int ans = 0;
    do ans = max(ans,max_num(a));
    while (next_permutation(a,a+9));

    cout << ans << endl;

    return 0;
}