This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
This is a Brilliant ( lol , get it ? ) question on A.P .... You can look at it from a different perspective. We have 10 A.P's with the same common difference 1 , A variable Initial term ( a ) and a variable Final term ( l ) = a + 9
S 1 0 = 5 ( a + a + 9 ) ⟹ 1 0 a + 4 5
we need to find
r = 1 ∑ 1 0 1 0 r + 4 5 = 5 5 0 + 4 5 0 = 1 0 0 0
By symmetry across the center, the average of the entries is 10, and the sum is 1 0 × 1 0 × 1 0 = 1 0 0 0
sir can you please elaborate some more on it
Log in to reply
If we consider any two entries that are symmetric with respect to the center of the grid, then a + b = 2 0 , so that the average comes out to be 10.
Alternatively, you can think of it as forming 50 pairs with a sum of 20 each, in the spirit of Gauss.
This answer is ingenious in its simplicity. We can tell by a glance that the average of each square is 10. So: Sum of sqrs / # of sqrs = 10 ...leading us to... Sum of sqrs = 100 x 10
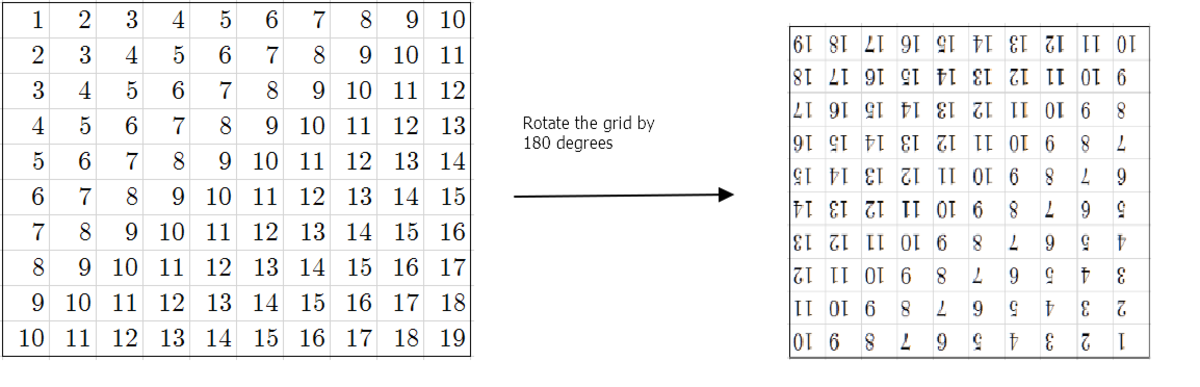
Let S denote this sum. If we rotate this grid as shown above, then adding their numbers in their respective cells shows that all their terms are 20.
Then 2 S is equal to the sum of all the numbers in the grid below.
⎣ ⎢ ⎢ ⎢ ⎡ 2 0 2 0 ⋮ 2 0 2 0 2 0 ⋮ 2 0 … … ⋱ … 2 0 2 0 ⋮ 2 0 ⎦ ⎥ ⎥ ⎥ ⎤
Hence, since there's a total of ten 20's in each rows and columns, then 2 S = 1 0 × 1 0 × 2 0 ⇒ S = 1 0 0 0 .
Fantastic solution, best yet!
just fabulous!!
Adding the numbers on opposing ends, we have:
S = ( 1 + 1 9 ) + 2 ( 2 + 1 8 ) + 3 ( 3 + 1 7 ) + . . . + 9 ( 9 + 1 1 ) + 1 0 ( 1 0 ) = n = 1 ∑ 9 2 0 n + 1 0 0 = 2 9 ( 1 0 ) ( 2 0 ) + 1 0 0 = 9 0 0 + 1 0 0 = 1 0 0 0
think from any row or column. the pattern is 55+65+75+85...................(just calculate first 2 or 3 terms. you will guess the easy pattern)
so, the summation is 1000.
Opposing numbers from one end of the grid to the opposite (numbers 1 and 100, 2 and 99.... all equal 20. There are 50 pairs of such numbers all equaling 20. 50 x 20 = 1000.
The sum
= 1 + 2 ( 2 ) + 3 ( 3 ) + 4 ( 4 ) + 5 ( 5 ) + 6 ( 6 ) + 7 ( 7 ) + 8 ( 8 ) + 9 ( 9 ) + 1 0 ( 1 0 ) + 1 1 ( 9 ) + 1 2 ( 8 ) + 1 3 ( 7 ) + 1 4 ( 6 ) + 1 5 ( 5 ) + 1 6 ( 4 ) + 1 7 ( 3 ) + 1 8 ( 2 ) + 1 9 = 2 0 + 2 ( 2 + 1 8 ) + 3 ( 3 + 1 7 ) + 4 ( 4 + 1 6 ) + 5 ( 5 + 1 5 ) + 6 ( 6 + 1 4 ) + 7 ( 7 + 1 3 ) + 8 ( 8 + 1 2 ) + 9 ( 9 + 1 1 ) + 1 0 0 = 2 0 ( 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 ) + 1 0 0 = 2 0 ( 4 5 ) + 1 0 0 = 9 0 0 + 1 0 0 = 1 0 0 0
The elements of the left to right diagonal line multiplied in number of elements of one row then it is 100*10=1000 Or Number of elements in the row ^3. Then it is 10^3=1000
So I fancied writing some code to do this. I wrote int xzult = 0; for (int j = 0; j<10; j++){ for (int i = 1; i<=10; i++){ xzult = xzult + i + j; System.out.print(i+j + " "); //print the grid } System.out.print("\n"); } System.out.println(xzult); //print the final number }
Top row and rightmost column sum to 190 =19*10.
Remove those numbers and repeat, you get 170 = 17*10.
Keep going until 10 = 10*1.
Summing you get: 10 (1+3+5+...+19) = 10 (100) = 1000 ,
1+2 2+3 3+4 4+5 5+6 6+7 7+8 8+9 9+10 10+11 9+12 8+13 7+14 6+15 5+16 4+17 3+18*2+19=1000
Relevant wiki: Sum of n, n², or n³
The sum of the first column is the tenth triangular number ( 1 + 2 + 3 . . . + 1 0 ), which can be worked out using 2 1 1 0 ( 1 0 + 1 ) = 5 5 . The sum of the second column is equal to 5 5 + 1 0 , since all ten number have been increased by one. The third is equal to 5 5 + 2 0 , and so on up to the tenth column. The sum of all the added on multiples of ten is thus 1 0 + 2 0 . . . + 9 0 , which is equal to 1 0 ( 2 1 9 ( 9 + 1 ) ) = 4 5 0 . The sum of all the original triangle numbers is just 5 5 × 1 0 = 5 5 0 . Therefore the answer is 5 5 0 + 4 5 0 = 1 0 0 0 .