GRIN
Consider a cylindrical optical fiber with a core that has a graded index (GRIN) of refraction given by where is the distance to from the optical axis of the fiber. Show that this profile results in continual refocusing of paraxial rays as shown in the figure below. If , determine the distance in millimeters between two consecutive focal points.
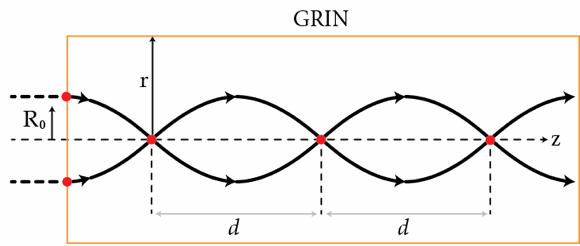
The answer is 9.52.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
As far as I can see, there is one obvious way of working this out which is to approximate the fiber as a series of infinitesimally thin layers between which, Snell's law applies. The relation is then Taylor expanded for a small change in r and a small change in θ from which an expression for d x 2 d 2 r is obtained and can be used to find the distance d which passes between intercepts of the focused rays.
However, that misses the chance to enjoy a beautiful technique from the calculus of variations. Variational calculus can be used to carry out generalized minimizations away from functions defined on a parameter space of variables, into functions defined on a space of functions. In other words, given a quantity defined as a function of a function such as a trajectory through space, one can search over the space of all such possible trajectories to find the right one.
Relying on Snell's law also undersells the underlying physics of photons in that it gives an impression that photons are particles which will travel in straight lines. Photons aren't localized particles and can't be shot like bullets at a target. The reality is something more subtle, photons are wavelike particles which are able to sample many different paths, with the observed path corresponding to that which has the strongest coherence. Paths which lead to phase mixing and interference are poorly represented. This picture, from quantum electrodynamics agrees with the 400 year old principle of Fermat which states that in traveling between two points in space, a light beam will take the path of shortest time.
What this also means is that light will travel on a trajectory which represents a minimum in trajectory space for the time taken. Paths infinitesimally displaced from such an optimal path will have the smallest phase difference with a bundle of neighboring paths. Path bundles with the smallest difference in phase will interfere the least and therefore result in the strongest signal from all path bundles in the trajectory space. All this is to say is that the true path of the photons can be found by finding the path of least time. In working that out we'll also be able to prove Snell's law as a free gimmick along the way.
Another shortcoming of the Snell's law approach occurs at the turnaround points. At some point in the curving trajectory, the particle has to turn around and therefore will have an angle of zero with respect to the horizontal. A straightforward application of Snell's law in this situation predicts that the light will continue on moving in a straight line because it will be moving in a layer of constant index of refraction.
In a medium with index of refraction n , the speed of light is given by c / n . Therefore, to go a distance s along a path in a media of homogenous index of refraction, the time taken would be s n / c . More generally, for a given path, the total time required is given by
t = i ∑ Δ s i n / c = c − 1 x a ∫ x b n ( r ) d s
For sake of argument, consider a beam of light which enters the waveguide at the origin ( r = 0 ) and crosses the x -axis at x = x f . One slow path the light could take would be to go directly from the origin to ( x = x f , r = 0 ) in a straight line. If it did, it would be traveling the entire path in the region of the highest index of refraction and therefore the lowest velocity. The light can clearly make a shorter trip by spending some portion of the trip in regions of lower index of refraction.
Let's pick two arbitrary endpoints for a portion of the path, ( x 0 , r 0 ) and ( x t 1 , r t 1 ) , covering t = 0 to t 1 . According to Fermat's principle, the light will follow a path between these two points such that the time taken is minimized. Again, the time required is related to the path by
t 1 = c − 1 0 ∫ t 1 n ( r ) d s
The path element d s is along the path itself but can be written in terms of the change in x and r :
d s = d x 2 + d r 2 = 1 + ( d r / d x ) 2 d x
The time taken is then
t 1 ( r ( x ) ) = c − 1 0 ∫ t 1 n ( r ) 1 + ( d r / d x ) 2 d x = c − 1 0 ∫ t 1 n ( r ) 1 + r ′ 2 d x
The problem is then to find the path r ( x ) which minimizes the integral above with respect to variations in the path. In short, the idea is that any small continuous disturbance around the optimal path such that the path still cuts through the given endpoints will have no effect on the time taken, a similar idea to the derivative being zero at an ordinary minima. The difference in time due to an infinitesimal disturbance along the optimal path must be zero. This argument leads to an expansion in the total derivative of the integral which can in general depend on r as well as r ′ . A very specific derivative relationship must be satisfied by the integrand I for the minimum path, namely
d x d d r ′ d I = d r d I
The details of the variational calculus of this kind of minimization are somewhat subtle but are derived at calculus of variations . In any case, this is the essential idea.
Now, the path will be fixed by the solution of the derivative relationship for our particular integrand, n ( r ) 1 + r ′ 2 , i.e.
d r d n ( r ) 1 + r ′ 2 = d x d d r ′ d n ( r ) 1 + r ′ 2 .
The left hand side is simple and is given by n ′ ( r ) 1 + r ′ 2 .
The right hand side becomes
1 + r ′ 2 r ′ ′ n ( r ) + 1 + r ′ 2 n ′ ( r ) r ′ 2 − ( 1 + r ′ 2 ) 3 / 2 n ′ ( r ) r ′ 2 r ′ ′
We can boil this down a bit and get a simple equation for r ′ .
n ′ ( r ) 1 + r ′ 2 n ′ ( r ) ( 1 + r ′ 2 ) 2 n ′ ( r ) ( 1 + r ′ 2 ) = 1 + r ′ 2 r ′ ′ n ( r ) + 1 + r ′ 2 n ′ ( r ) r ′ 2 − ( 1 + r ′ 2 ) 3 / 2 n ′ ( r ) r ′ 2 r ′ ′ = ( r ′ ′ n ( r ) + n ′ ( r ) r ′ 2 ) ( 1 + r ′ 2 ) − n ( r ) r ′ 2 r ′ ′ = r ′ ′ n ( r )
The last line can be written as an exact differential by dividing through by 1 + r ′ 2 :
n ′ ( r ) ( 1 + r ′ 2 ) d r d n ( r ) 1 + r ′ 2 = r ′ ′ n ( r ) = 0
Pausing for a moment, we see that this is a proof of Snell's law for the bending of light at an interface of two materials. To see this, we solve the equation and see that 1 + r ′ 2 n ( r ) = C where C is a constant. This means that along the entire path, the quantity 1 + r ′ 2 n ( r ) must be constant. d r is the vertical displacement of the light beam and d x is the horizontal displacement of the light beam.
In the case of two materials with a horizontal interface, the angle between the hypotenuse and the displacement d r is the angle of interest in Snell's law where the angle is measured between the vertical and the light path (the hypotenuse here). In that case the base is given by d x , the hypotenuse by d x 2 + d r 2 and sin θ by d x 2 + d r 2 d x = 1 + r ′ 2 1 . Therefore, the derivative relation above reduces to Snell's law at the boundary of two mediums.
Now, we'll use the derivative relation to solve for the path in the GRIN medium.
As we showed above, the relation implies n ( r ) = γ 1 + r ′ 2 where γ is some constant. Evaluating at r = 0 we see that is must be n 0 .
Again, using the relation, we see that
r ′ ′ = ( 1 + r ′ 2 ) n ( r ) n ′ ( r ) = n ( r ) n ′ ( r ) n 0 2 n ( r ) 2 = n 0 2 n ′ ( r ) n ( r )
Given the form of the index of refraction given for the optical fiber, we have
r ′ ′ = n 0 n 0 1 − g 2 r 2 2 1 n 0 1 − g 2 r 2 − 2 g 2 r = − g 2 r
I.e. d x 2 d 2 r = − g 2 r
This means that the points on the path will follow an oscillatory trajectory along the x axis with wavenumber g . This also means that the possible paths are restrained. The path can be made to have differing amplitudes but it will always follow a sinusoidal path with the given wavenumber, which means that all trajectories will have the same intercepts along the axis. In traversing the distance d the phase is increased by p i , therefore we want to find d such that d g = π , which gives the result d = g π .