Groovy groove
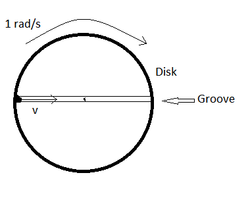 We have a disk of mass
M
and radius
R
placed on a horizontal plane. A cylindrical groove of radius
r
is made on a diameter.Now a sphere of mass
m
and radius
r
is placed in the groove at the circumference of the disk.
We have a disk of mass
M
and radius
R
placed on a horizontal plane. A cylindrical groove of radius
r
is made on a diameter.Now a sphere of mass
m
and radius
r
is placed in the groove at the circumference of the disk.
At t = 0 the whole system is rotated with an angular velocity 1 r a d / s as shown in the figure.Also at the same time the sphere was projected with a velocity v towards the centre of the disk.Find the minimum velocity v of the sphere such that it is able to reach the other end of the groove.
Details and Assumptions
1 ) r ≪ R
2 ) M = 2 k g
3 ) m = 3 K g
4 ) R = 2 m
5 ) The disk is fixed about it's centre that is it can only rotate
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice solution bro. :)
Log in to reply
Thanks, yours is nice too
Same soln. Can be generalised for other bodies too
If the ball crosses the center of the disk then the centrifugal force will be enough to move that ball to the other side of the groove. I think the minimum velocity in this case is the velocity which is enough to move the ball to the center of the disk. Initial energy of the system= 2 m v 2 + 2 I B ω ‘ 2 + 2 I D ω 2
Initial energy of the system is in the form of kinetic energy of the ball + rotational energy of the ball+rotational energy on the disk.
Final energy of the system will be in the form of rotational energy of the disc.
Final energy of the system= E f = 2 I f ω f 2
By law of conservation of angular momentum I i ω i = I f ω 2
So ω f = M R 2 M R 2 + 2 m R 2 On equating initial and final energies I got
2 3 v 2 + 2 m R 2 + 4 M R 2 = 4 1 6 M R 2
2 3 v 2 + 8 = 3 2
So v=4m/s
Hey Satvik you are just 15 and you know so much about physics, you are a genius! keep it up and always try to reach new heights. All the best!
I forgot to mention the value of moment of inertia. Here it is
I B = m R 2 , I D = 2 M R 2 , I f = 2 M R 2
Thank you Ronak for posting this question.
Log in to reply
Good solution.
I too have done the same way.
Thank you very much bro. :)
Thank you Ronak.
If the ball wants to move to the other side of the groove, it should just cross the center of the disc as the centrifugal force will carry it to the other side on its own. so we need to apply work energy theorem or the mechanical energy conservation from the starting point to the center and also the conservation of angular momentum. And the solution goes as Satvik Pandey has specified in his solution!
Use the fact that the ball just needs to cross the centre so that the centrifugal force is enough to get the ball to the otherside. Then use angular momentum conservation and kinetic energy conservation.
You don't need to use conservation of energy. Here is my solution without it:
Let me define the variable x to be the distance between the ball and the center of the disk.
The initial angular momentum is 1 6 , and the rotational inertia as a function of the balls position, x, is 4 + 3 x 2 therefore the angular velocity as a function of the ball's position is:
ω = 4 + 3 x 2 1 6
The acceleration (from the centrifugal force) on the ball as a function of it's position is:
α = − ω 2 x = − x ( 4 + 3 x 2 1 6 ) 2 = d t d V = d x d V d t d x = V d x d V = 2 1 d x d ( V 2 )
We're looking for the minimum necessary velocity, which implies v=0 when x=0
∫ 2 0 d ( V 2 ) = Δ V 2 = V 2 = ∫ 2 0 ( 3 x 2 + 4 ) 2 − 5 1 2 x d x = [ 3 ( 3 x 2 + 4 ) 2 5 6 + C ] 2 0 = 1 6
And so V = 4 m/s