Grounded Sphere
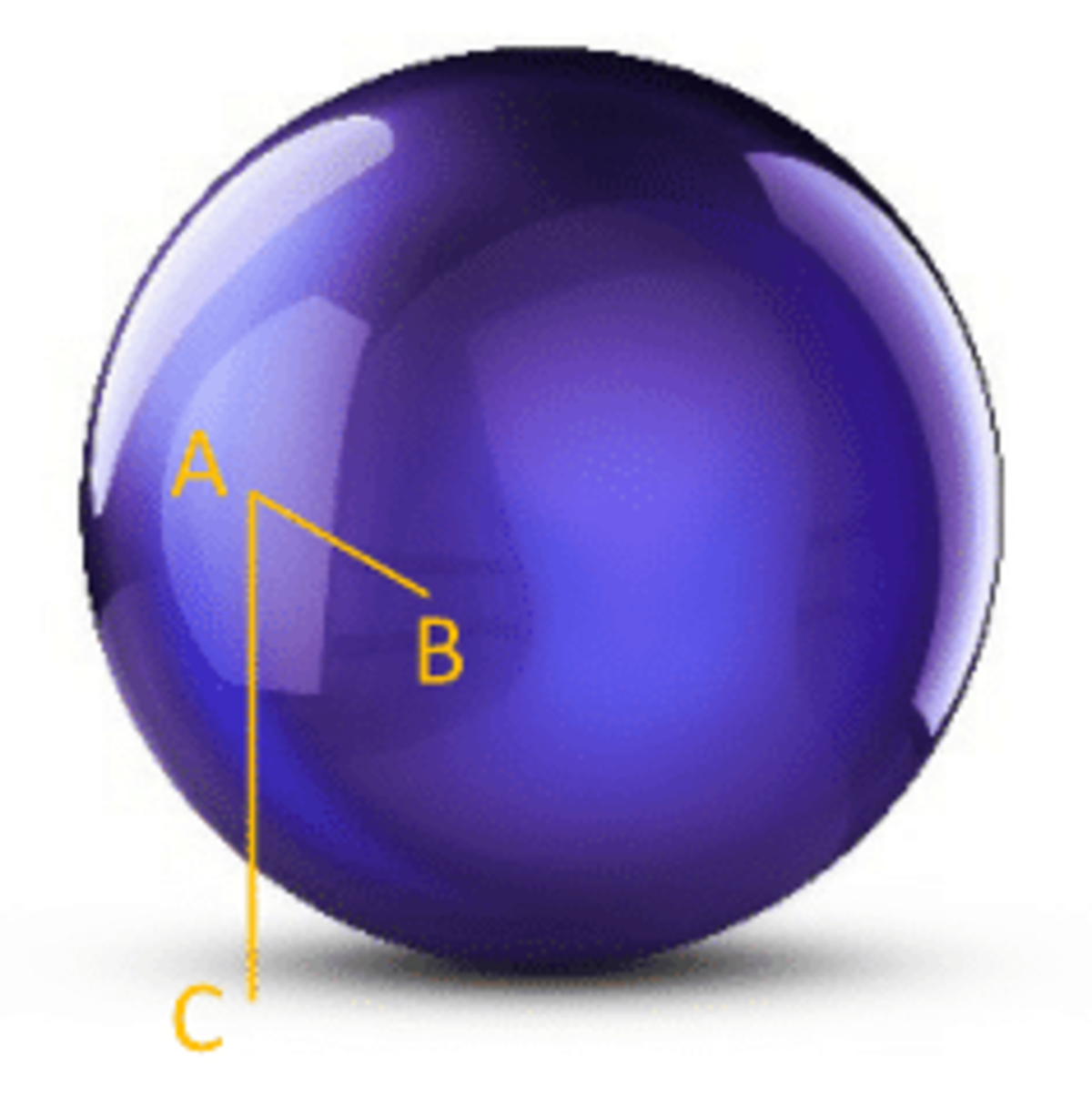
Sphere with a diameter is resting on a horizontal plane. A and B are points on the surface of the sphere. Point A is 9 cm off the ground, the straight line distance is , and the tangent of the angle is 7. Find the difference between the smallest and the largest possible values of .
Image of sphere from kingofwallpapers.com.
The answer is 1680.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This is a 2D problem in a 3D disguise. The center of the smallest possible sphere is directly below the line connecting A and B, while the center of the largest possible sphere is directly above that line. We can picture the plane in which all of this is happening and set up a coordinate system in it.
The coordinates of point A are (0, 9). The ratio of DB to DA, which is the tangent of angle BAC, is 7. If we set DB = 7 and DA = 1 that would be the easiest way to satisfy this requirement. This will give us the A B = 5 0 as required. Coordinates of point B are therefore (7, 8).
The center of the sphere needs to be a distance R from: (1) point A, (2) point B, and (3) the ground. This gives us three equations:
x 2 + ( y − 9 ) 2 = R 2
( x − 7 ) 2 + ( y − 8 ) 2 = R 2
y = R
Solving for R we get two answers: R = 5 and R = 8 4 5 . The difference of the diameters is therefore quite a large figure, namely 1680.