Groundwork
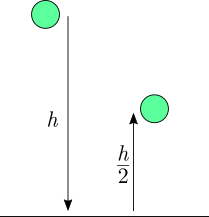
A ball is dropped from height , hits the ground with speed , and bounces back to a height . If the mass of the ball is , how much energy is dissipated to the ground by the ball?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Understanding the work-kinetic energy theorem
Let the work done by the ground be W g . We can use the work-kinetic energy theorem to solve this problem.
The initial and the final states of the object can be picked according to our convenience. Suppose the initial state is chosen when the ball is dropped, and the final state is when the ball reaches its highest point after the bounce. In both cases, the speed of the ball is zero. This implies that the change in kinetic energy is zero, and the total work done on the ball by net force during this motion is zero.
Note that during this motion, the only forces acting on the ball are the gravitational force, and the impulsive normal reaction when the ball hits the ground. The difference between the initial and final heights of the ball is h − 2 h = 2 h . Hence the work done by gravitational force is m g 2 h . We get the equation:
W g + 2 m g h = 0
We can apply conservation of energy during the descent of the ball to get m g h = 2 1 m v 2 . Substituting this in the above formula gives
W g = − 2 m g h = − 4 1 m v 2