Group or not?
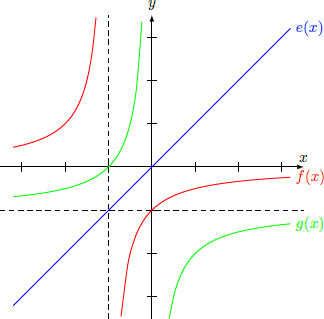
Given are the functions e ( x ) f ( x ) g ( x ) e , f , g : = x = − 1 + x 1 = − 1 − x 1 R ∖ { − 1 , 0 } → R ∖ { − 1 , 0 } Is the set G = { e , f , g } together with the function composition f 1 ∘ f 2 = f 1 ( f 2 ( x ) ) as operation a group?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We first calculate all possible operations between the elements of the set G . The element e is the identity e ( x ) = x , so that e ∘ h = h ∘ e = h for any function h ( x ) . We must calculate only the operations between the elements f and g : f ( f ( x ) ) f ( g ( x ) ) g ( f ( x ) ) g ( g ( x ) ) = − 1 − 1 + x 1 1 = − 1 − 1 + x 1 1 1 + x 1 + x = − 1 + x − 1 1 + x = − x 1 + x = − x 1 − 1 = g ( x ) = − 1 − ( 1 + x 1 ) 1 = − − x 1 1 = x 1 1 x x = x = e ( x ) = f ( f ( f ( x ) ) ) = f ( g ( x ) ) = e ( x ) = f ( f ( g ( x ) ) ) = f ( e ( x ) ) = f ( x ) Here we can extend the fractions with the terms x and x + 1 , since these are non-zero for x ∈ R ∖ { − 1 , 0 } . In lines 3 and 4 we took advantage of the associativity of the composition ∘ . The results can be summarized in the following Cayley table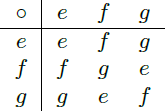 So we can summarize the results as follows:
So we can summarize the results as follows:
Since the operation ∘ is also associative, all group axioms are satisfied. The group ( G , ∘ ) is isomorphic to the group D 3 .