Grumpy Quadrilateral

Let $\angle ABD = \angle BCD = \alpha$ and $\angle BDC = \beta$ . Then $\angle ADB = \angle ABD + \angle BDC = \alpha+\beta$ . Split $\angle ADB$ by $DE$ such that $\angle ADE = \alpha$ and $\angle BDE = \beta$ . Then $\angle DEA = \angle DBE + \angle BDE = \alpha + \beta$ .

We note that $\triangle ADE$ and $\triangle ABD$ are similar. Then $\dfrac {AE}{AD} = \dfrac {AD}{AB} = \dfrac 58 \implies AE = \dfrac 58 \cdot AD = \dfrac {25}8$ . Also $\triangle BCD$ and $\triangle BDE$ are similar and

$\frac {BC}{BD} = \frac {BE}{DE} \implies BC = BE \cdot \frac {BD}{DE} = BE \cdot \frac {AB}{AD} = \left(8-\frac {25}8 \right)\frac 85 = \boxed{\frac {39}5}$

Let $\angle ABD= \alpha$ and $\angle BDC= \beta$ , we are given that $\angle BCD=\alpha$ and $\angle ADB=\alpha +\beta$ .

By the alternate segment theorem , $AB$ is tangent to the circumcircle of $\triangle BDC$ at point $B$ .

Construction: Draw the circumcircle of $\triangle BDC$ and extend $AD$ to $E$ such the point lies on the circle.

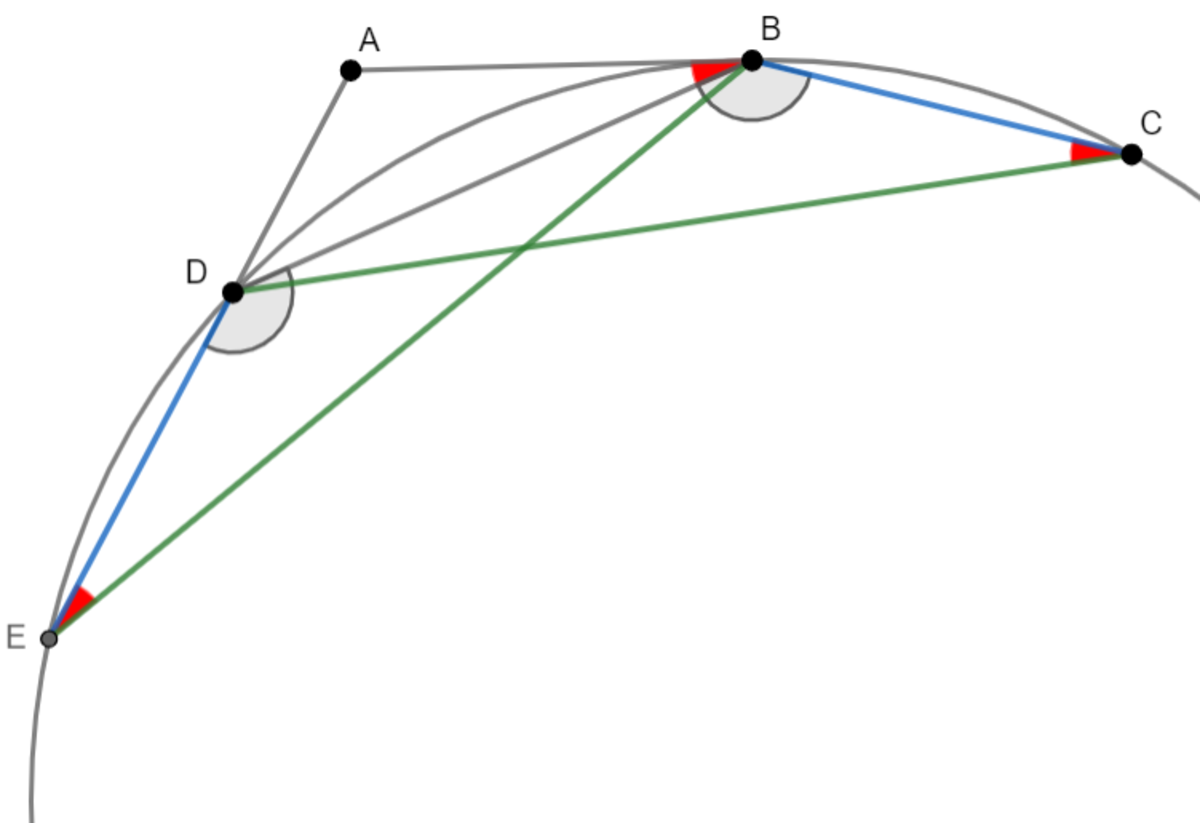
Simple angle chasing leads to $\angle BDE=\angle DBC= 180-\alpha -\beta$ Since quadrilateral $BDEC$ is cyclic , $\angle DEB=\angle BCD =\alpha$ From the above results, it is easy to see that $\triangle BDE\cong \triangle DBC \implies DE=BC$ Applying the tanget-secant theorem , $AD\cdot AE=AB^2\implies AD\cdot (AD+DE)=AB^2\implies DE=BC=\frac{AB^2-AD^2}{AD}$ Substituting the given values for $AD$ and $AB$ , $\boxed{BC=\frac{8^2-5^2}{5}=\frac{39}{5}}$