Hail Stewart-1!

Geometry Level 3

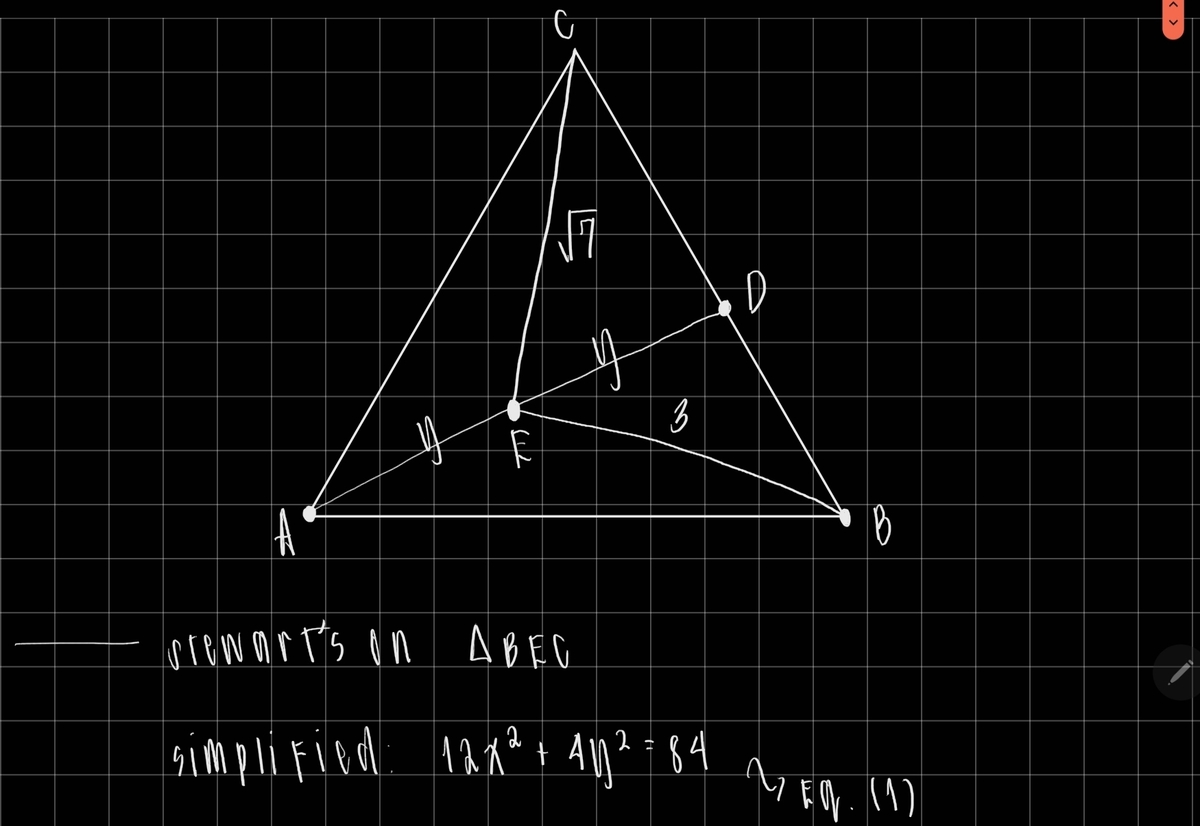
In $\triangle ABC$ , $AC=BC$ , point $D$ is on $BC$ such that $CD=3\times BD$ , and $E$ is the midpoint of $AD$ such that $CE=\sqrt 7$ and $BE=3$ .

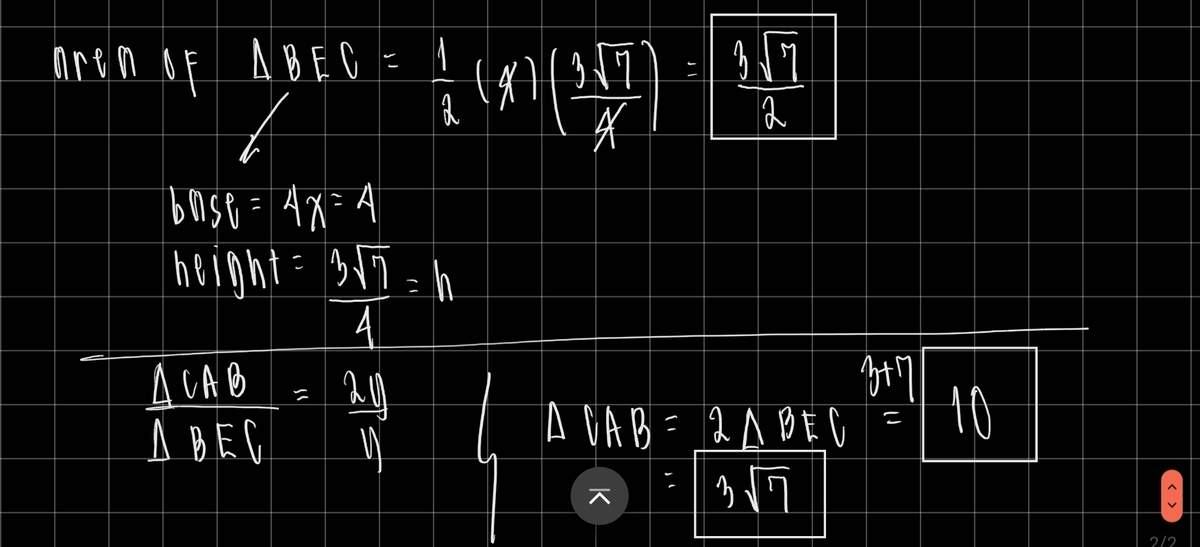
If the area of $\triangle ABC$ is $m\sqrt n$ , where $m$ and $n$ are positive integers and $n$ is square-free, find $m+n$ .

The answer is 10.

2 solutions

김 재형
Apr 15, 2018

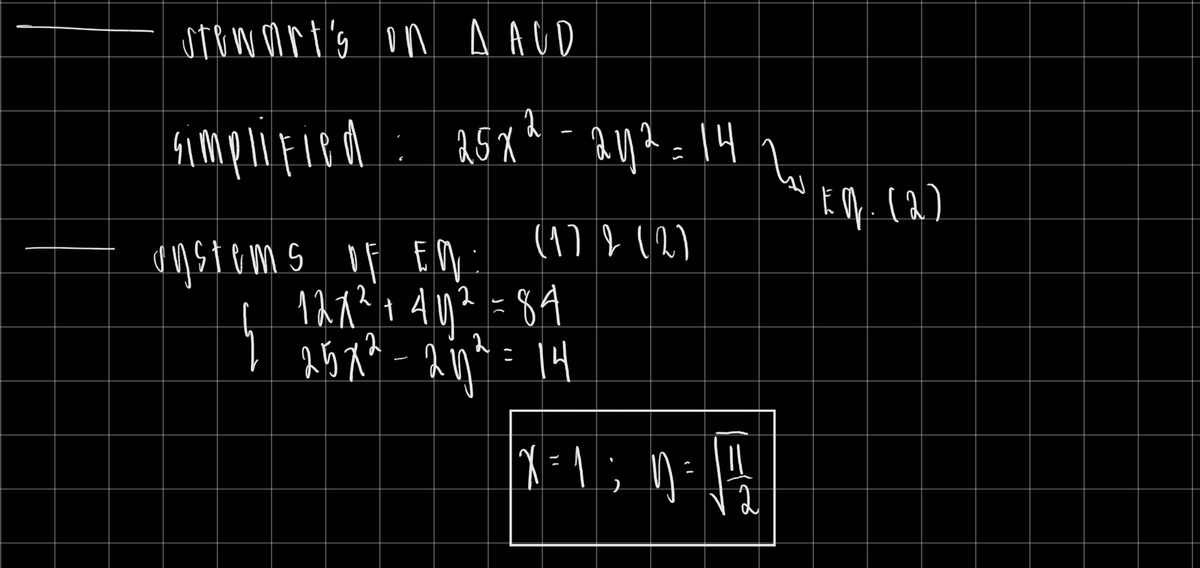
Heh, I'm the first!!! :D

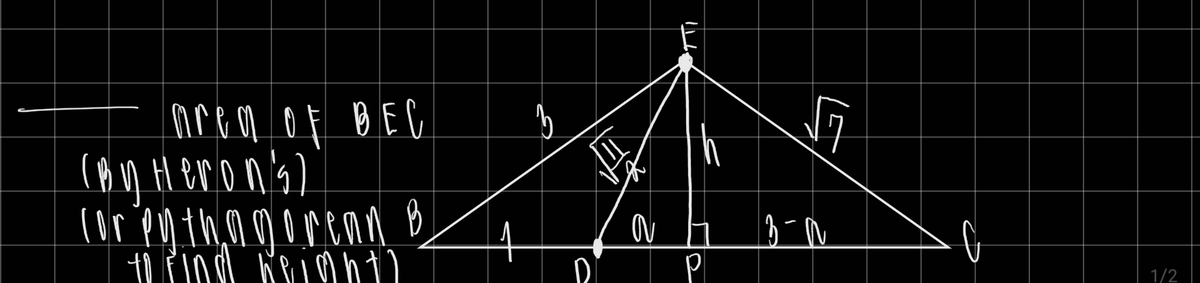
Since length of all three sides have been found, the area of the triangle can easily be calculated, either through Heron's formula or by using the properties of isosceles triangles. The area is 3*sqrt(7), and since both 3 and 7 are positive integers and n is square-free, m+n = 10.