Halbach Magnet
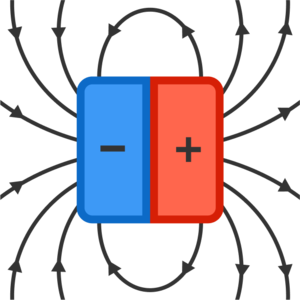
Johnny and Klaus engineer an array of magnets in the following pattern:
Is the magnetic field stronger on side A or B?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
The problem is ill-defined. I believe the magnetic flux density on both sides should be equal on the surface, but the rate of decrease with distance from the surface will be greater on side A
Log in to reply
Can you elaborate why this is true?
Log in to reply
The reason I think this is true is that on the surface of the magnet the effect of that magnet is much stronger than the competing effects of other more distant magnets. Similar to an electric field out of a point charge or the magnetic field infinity close to a current carrying wire. I may be erring though, as my understanding of permanent magnets is not that great.
You are correct , the line count on the surface is EQUAL for side A and B.
The magnetic field from each magnet is present everywhere, so the net field at the surface of each magnet will not be equal to the net field at the surface of any of the others because there is no symmetry operation you can perform on the entire configuration that transforms it into itself.
According to this diagram, I think it shows your statement about equal strength on the surface to be inaccurate, though I'm not certain: https://en.wikipedia.org/wiki/Halbach array#/media/File:Halbach array_field.jpg
Regardless of the answer, the question itself is not worded clearly because knowing the magnitude of the magnetic flux density requires you to specify a POINT, not a region. Comparing the magnetic fields requires telling us 2 points, not two regions. The question is worded in that typically imprecise way that physics textbook homework problems are worded, which leaves most students frustrated, and leaves some hating physics.
Log in to reply
Agree! If you integrate the magnetic field over the surface you can see that the question is not clear...
Log in to reply
Just another reminder that most people don't know the difference between magnetic field and magnetic flux density.
Clearly, the two sides of the magnetic array aren't the same and so does their magnetic field. On one side the field is much stronger than the other that is why it makes sense to generally compare the two sides. Such a magnet is used as refrigerator magnets which stick strongly only through one side.
The magnetic flux density is not uniform in the entire region A. However, you can take any point in region A and compare it with the symmetrically opposite point in region B.
The Red or Blue areas are EQUAL on either side A or B. Thus the line count is the SAME.
Log in to reply
Line count isn't the same because it represents the magnitude of the NET field at each point, and the corresponding vector is the vector sum of the magnetic fields from all of the magnets. This is mathematically similar to how the net electric field at a specified point is the net vector sum of the electric fields from multiple point charges at that same point. I felt the problem was poorly worded because one can always find a point in region B where the magnitude of the net field is smaller than it is at some selected point in region A. However, there are far more pairs of points where the opposite is true, and that's why "region B" is reported as the correct answer.
Field lines are only visual representations of a field. The density of field lines is a proportiobal representation of field strength, but does not actually represent where the field is, because the field is everywhere, so there are infinite lines a positive particle would travel. I think you are still on to the right concept, but using a "fixed number of field lines" as though that is a real, measurable physical quantity mistakes representation for reality.
Locally, the magnetic fields on side B are stronger, but from a distant point the field strengths are equivalent because the number of poles is equal on both side.
Yep. Halbach Arrays are often used in items like card holders or refrigerator magnets.
How do you pronounce Halbach?
In fact yes. It is a pity the Wikipedia article does not exist in French.
My guess would be that since side A has magnets alternating more frequently, the magnetic field is weakened. Similar to how magnetic fields are stronger when magnets of the same pole are less further apart.
Right, the density of field lines in side A is less because north and south poles are closer to each other, so the magnetic field is less strong there.
Log in to reply
Johnny and Klaus ;-) interesting question. Thanks Pranshu!
This arrangement is called the
Halbach Array
.
Ideally, the magnetic field nearly cancels out in one side of the magnets, and gets amplified on the other. This happens as a consequence of the sum of the magnetic fields of pairs of vertical and horizontal magnets:
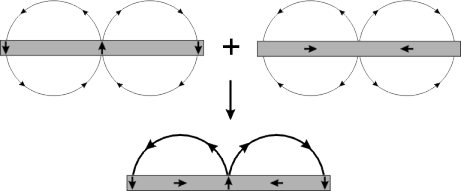
My view is that the field lines of the north and south pole is cancelled out on A side so it has no magnetic field and on the side B ,the magnetic field are doubled
The field lines are not totally cancelled out on A, but they are much weaker on A compared to B. This can be seen in this figure:
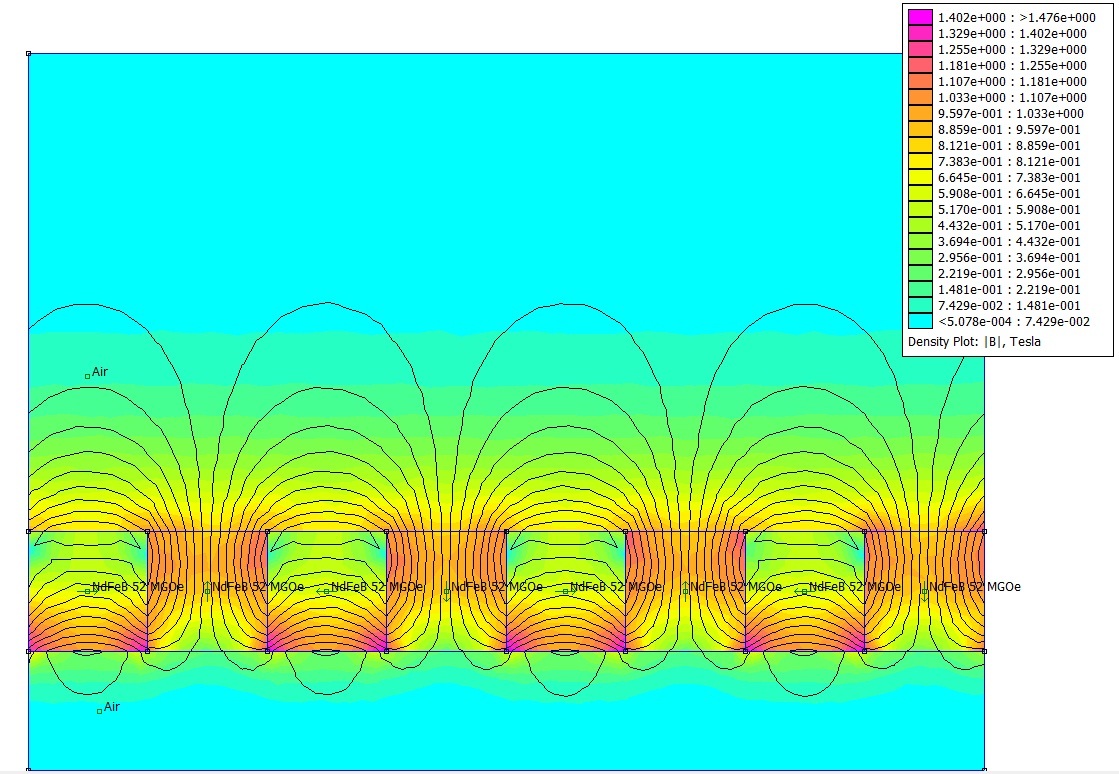
Concentrate on any group of three adjacent magnets, where one magnet has poles on right and left and two magnets have poles on the top and bottom. Sketch the field for all three magnets. Notice how the middle magnet (the one with a right and left pole) decreases the field strength from the other magnets on side A and increases the field strength on side B.
The answer to this question is B because there is a lack of cancellation of magnetic fields propagated outwards on this side, and in fact, an amplification instead. Egenriether has already mentioned that this is something called a Halbach Array, it is primarily a question on geometry and a little bit of arithmetic, if I have a positive value and a negative one, they detract from one another! This is pertinent to our case because if a field line pointing in the opposite direction to another run into one another, they’d cancel to some degree, thus, the field strength measured there will be a little weaker than if the two lines were to be left alone. In fancier terms, if I were to superpose two fields such that two lines pointing oppositely overlap, the net field is weaker than either one alone. The best exercise that I’d recommend is to actually draw some “model” field lines out of the array above, remembering that the orientation is such that lines always point away from positive ends and towards negative ends and that all lines are parts of closed loops that wrap back around to the magnet’s opposite side. If you do this, you’ll see that side B has lines that pretty much never cancel one another and in fact, the field lines are super posed in such a way that they are additive on side B, resulting in a strong magnetic field on this side. Side A, on the contrary, cancels plenty of field lines, resulting in quite a weak magnetic field. It’s easiest to see this starting from just one magnet, drawing the field lines, and then adding one on one side and another to the other in the way shown in the diagram, then see what happens when you add more field lines to incorporate the newly added magnets! This cancellation of fields is what the Halbach Array hinges on. Hope this helps! Fun fact, the reason why we or anything else besides permanent magnets are not inherently magnetic is because the magnetic fields of our electrons cancel one another, this is something called diamagnetism, iron and other permanent magnets exhibit paramagnetism, in which such a cancellation doesn’t happen since they have orbitals with just one electron so there isn’t another with opposing spin to cancel the field of the first. Once a bunch of these atoms align, the fields are added to result in a strong magnetic field, which is why iron is magnetic. There is more about the magnetism of iron but you can surely find this on Google, have a good day.
The way I got B is because of the Law of Electric Charges. Like charges repel, unlike charges attract. That means if there is 2 negatives or 2 positives forced to be next to each other, the magnetic field pushing against each of the magnets will most definitely be stronger. If the magnets are alike there will not be any resistance, or push between each magnet.
Field lines from adjoining and opposite poles cause near zero magnetic field - the majority of the field is concentrated at the contact surfaces. By contrast the field lines from adjoining common poles is forced out strongly as they repel each other. In particular the three identical poles force the center magnet field lines outward a great distance before they can loop around the field lines of the magnets hemming them in on either side.
A simple idea is to consider how the magnets pair up.
If you have a magnet with north at the top, south at the bottom, the field lines circle around going out the top around, down the side, then round and in the bottom. If you have a magnet on its side, with north to the right, then the liens go out to the north, then outwards (up and down), back to the left then in to the centre and then to the right into the pole.
If this sideways magnet is placed to the right of the upright magnet (as in the diagram), then the field lines from the vertical magnet is going up just above and below. In the same region the field lines from the horizontal magnet are going inwards towards the middle. This is downwards at the top and upwards at the bottom.
The up and down at the top oppose each other reducing the strength. The up and up at the bottom are aligned and support each other, increasing the strength.
The easiest way to figure this one out is to notice the positioning of each magnet. The B side of the same type are repulsing one another due to their U shape; all the while being attracted to its opposite in the center of that shape. If anyone actually tried this the magnets would have to be bolted down to keep them from moving about in a crazy manner.
PS I could be wrong, however I played a ton with magnets when I was a kid. I would chalk it up to experience on why I got it right, if that is the case.
The question as asked is nonsense; all finite sized magnets asymptotically are dipoles, and so is this. The distance was not specified, so sufficiently far away sides symmetrically located should have the same strength.
The density of the field lines encode the strength of the magnetic field at a given location in space.
A fixed number of field lines leave the + pole and a fixed number of them enter the − pole. The field lines on side A are more sparse because there are many opposing poles next to each other, so most lines just go directly into the nearby − poles. On the other hands, the field lines on side B gets to build up.