Half filled glass of water

Classical Mechanics Level 4

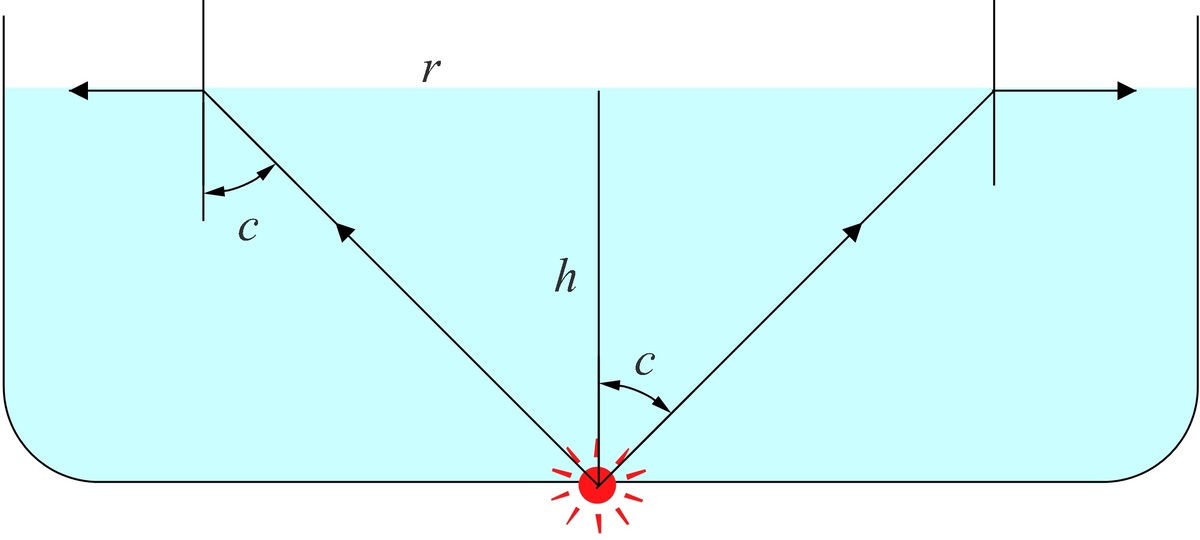
A point source of light is kept at the bottom of a cylindrical container of radius $R$ , half filled with water. It is seen that light emerges out of the top surface of water from a circular area of radius $r (<R)$ .

If water is poured in the container at a rate $\frac{dV}{dt} = Q$ then the radius of circular area will change at the rate $\frac{\sqrt{a}Q}{\sqrt{b}\pi R^2}$ where $a$ and $b$ are coprime positive integers, find the value of $a+b$ .

Take the refractive index of water as $\frac{4}{3}$ .

The answer is 16.

1 solution

Rohit Ner
Jan 23, 2016

$\begin{aligned}\sin c&=\frac{1}{\mu} \text{ (Snell's Law)}\\\tan c&=\frac{1}{\sqrt{{\mu}^2-1}}\\\frac{r}{h}&=\frac{1}{\sqrt{{\mu}^2-1}}\\\frac{dr}{dt}&=\frac{1}{\sqrt{{\mu}^2-1}}\frac{dh}{dt}\\\frac{dV}{dt}&=Q\\\pi{R}^2\frac{dh}{dt}&=Q\\\frac{dr}{dt}&=\frac{1}{\sqrt{{\mu}^2-1}}\frac{Q}{\pi{R}^2}\\&=\frac{1}{\sqrt{{\left(\frac{4}{3}\right)}^2-1}}\frac{Q}{\pi{R}^2}\\&\huge\color{#3D99F6}{=\boxed{\sqrt{\frac{9}{7}}\frac{Q}{\pi{R}^2}}}\end{aligned}$

Half filled glass of water

The answer is 16.

1 solution

0 pending reports