Half-Inscribed
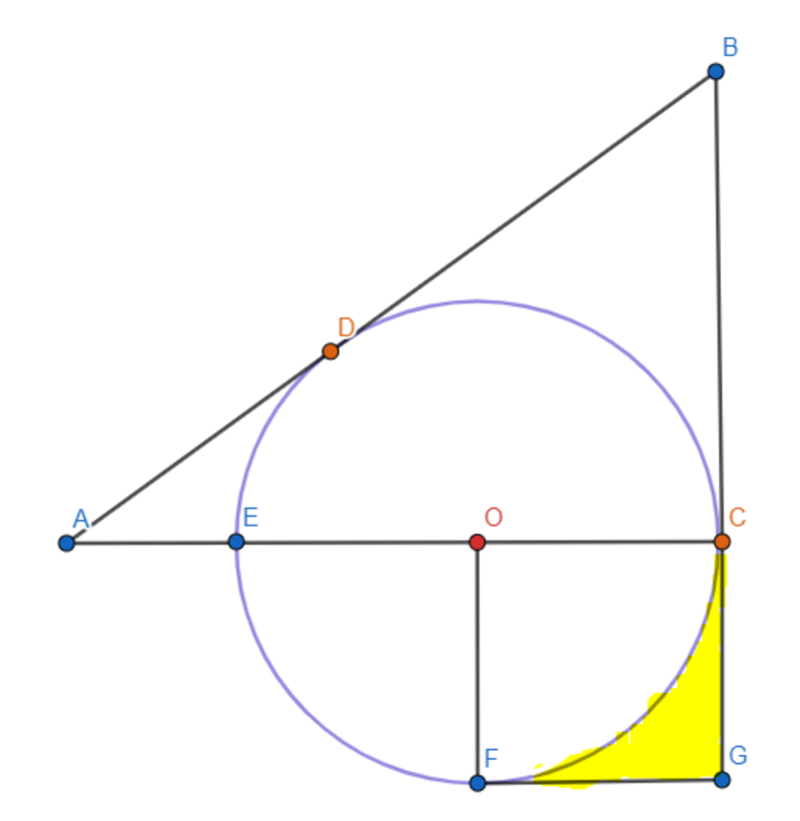
In the diagram above, B A and B G are tangents to the circle with center O at point D and C respectively. Minor sector C O F is a quarter circle and C O F G is a square.
Given that A D = 2 and the area of the shaded region C G F is 1 6 3 6 − 9 π , find B C .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Very well presented! I like your diagrams :)
Thank you!! 😊
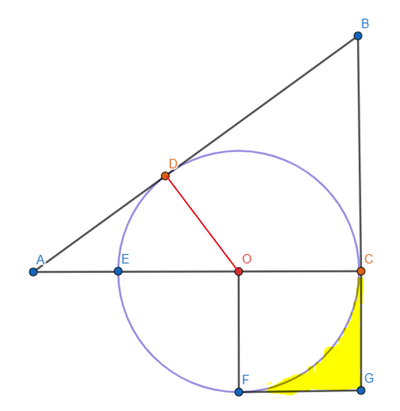
Let the radius of the circle be r . Then the side length of square C O F G is r and the area of the yellow region is
r 2 − 4 π r 2 1 6 r 2 − 4 π r 2 ⟹ r 2 r = 1 6 3 6 − 9 π = 3 6 − 9 π = 1 6 3 6 = 4 6 = 2 3
Now note that △ A B C and △ A O D are similar. Then we have
A C B C ⟹ B C = A D O D = A D O D × A C = A D O D ( A O + O C ) = A D O D ( O D 2 + A D 2 + O C ) = 2 2 3 ⎝ ⎛ ( 2 3 ) 2 + 2 2 + 2 3 ⎠ ⎞ = 4 3 ( 2 5 + 2 3 ) = 4 3 × 4 = 3
Let the radius of the circle =
x

Area of the shaded region x 2 − 4 π x 2 = 1 6 3 6 − 9 π x = 4 ( 4 − π ) 9 ( 4 − π ) = 2 3 Now , Join O D to get a right angle triangle
So , A D 2 + O D 2 = ( A E + E O ) 2 2 2 + ( 2 3 ) 2 = ( A E + 2 3 ) 2 A E 2 + 3 A E − 4 = 0 A E = 1 In triangle A B C , B D = B C = y ( they are tangent from the same point )
So , ( 2 + y ) 2 = ( 2 3 + 2 3 + 1 ) 2 + y 2 4 + 4 y = 1 6 y = 3
Refer to Ethan Mandelez's diagrams for this answer.
Let O C = r . Then r 2 − 4 1 π r 2 = 1 6 3 6 − 9 π ⇒ r 2 ( 1 − 4 1 π ) = 1 6 1 ( 3 6 − 9 π ) , so r 2 = 1 6 1 × 3 6 ⇒ r = 1 . 5 (since r cannot be negative).
Thus A D 2 + D O 2 = A O 2 , but since D O = r as well, A O = 2 2 + 1 . 5 2 = 2 . 5 .
Now here is where our solutions differ. Since Δ A O B and Δ B O C have the same height, through the formula A = 2 1 b h , the ratio of their areas must be the ratio of their bases. Thus:
Δ B O C Δ A O B = O C A O ⇒ 2 1 ( 1 . 5 ) ( x ) 2 1 ( 2 + x ) ( 1 . 5 ) = 1 . 5 2 . 5 ( tangents from the same point are equal : D B = C B = x ) ⇒ 1 . 5 x 3 + 1 . 5 x = 1 . 5 2 . 5 ( cancel and simplify )
and the rest is straightforward: ⇒ 1 . 5 ( 3 + 1 . 5 x ) = 2 . 5 ( 1 . 5 x ) ⇒ 4 . 5 = 1 . 5 x , x = 3 .
A really good approach!! Good job
No problem!