Half Of One Side, Third Of Another
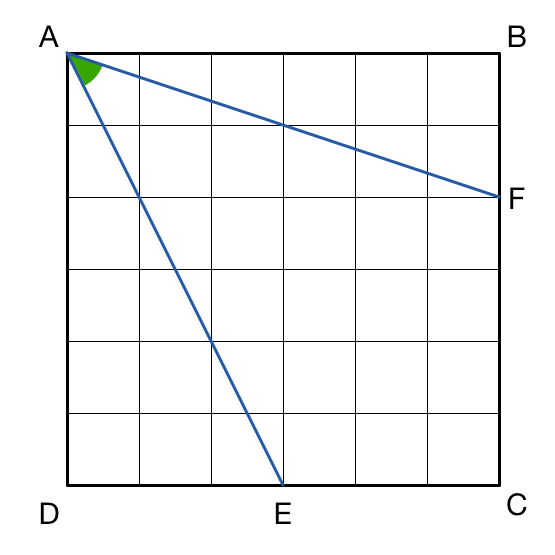
In square , is the midpoint of . lies on such that .
What is angle ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
With D being the origin of a grid with standard orientation, draw a line segment from F to P ( 2 , 2 ) . Then as P F has slope 2 1 and A P has slope − 2 we see that ∠ A P F = 9 0 ∘ . Also, as ∣ A P ∣ = ∣ P F ∣ = 2 5 we see that Δ A P F is a right isosceles triangle at P , and thus that ∠ P A F = 4 5 ∘ .
∠ E A F = 9 0 ∘ − ( ∠ D A E + ∠ F A B ) = 9 0 ∘ − ( tan − 1 ( 2 1 ) + tan − 1 ( 3 1 ) ) =
9 0 ∘ − tan − 1 ( 1 − 2 1 ∗ 3 1 2 1 + 3 1 ) = 9 0 ∘ − tan − 1 ( 1 ) = 4 5 ∘ ,
where the formula tan − 1 ( x ) + tan − 1 ( y ) = tan − 1 ( 1 − x y x + y ) was used.
Using the cosine rule and Pythagoras, we have that
∣ E F ∣ 2 = ∣ A E ∣ 2 + ∣ A F ∣ 2 − 2 ∣ A E ∣ ∣ A F ∣ cos ( ∠ E A F ) ⟹
2 5 = 4 5 + 4 0 − 2 4 5 4 0 cos ( ∠ E A F ) ⟹
cos ( ∠ E A F ) = 2 4 5 ∗ 4 0 6 0 = 9 ∗ 5 ∗ 4 ∗ 2 ∗ 5 3 0 = 3 0 2 3 0 = 2 1
⟹ ∠ E A F = cos − 1 ( 2 1 ) = 4 5 ∘ .