Half Ring Reaction Force
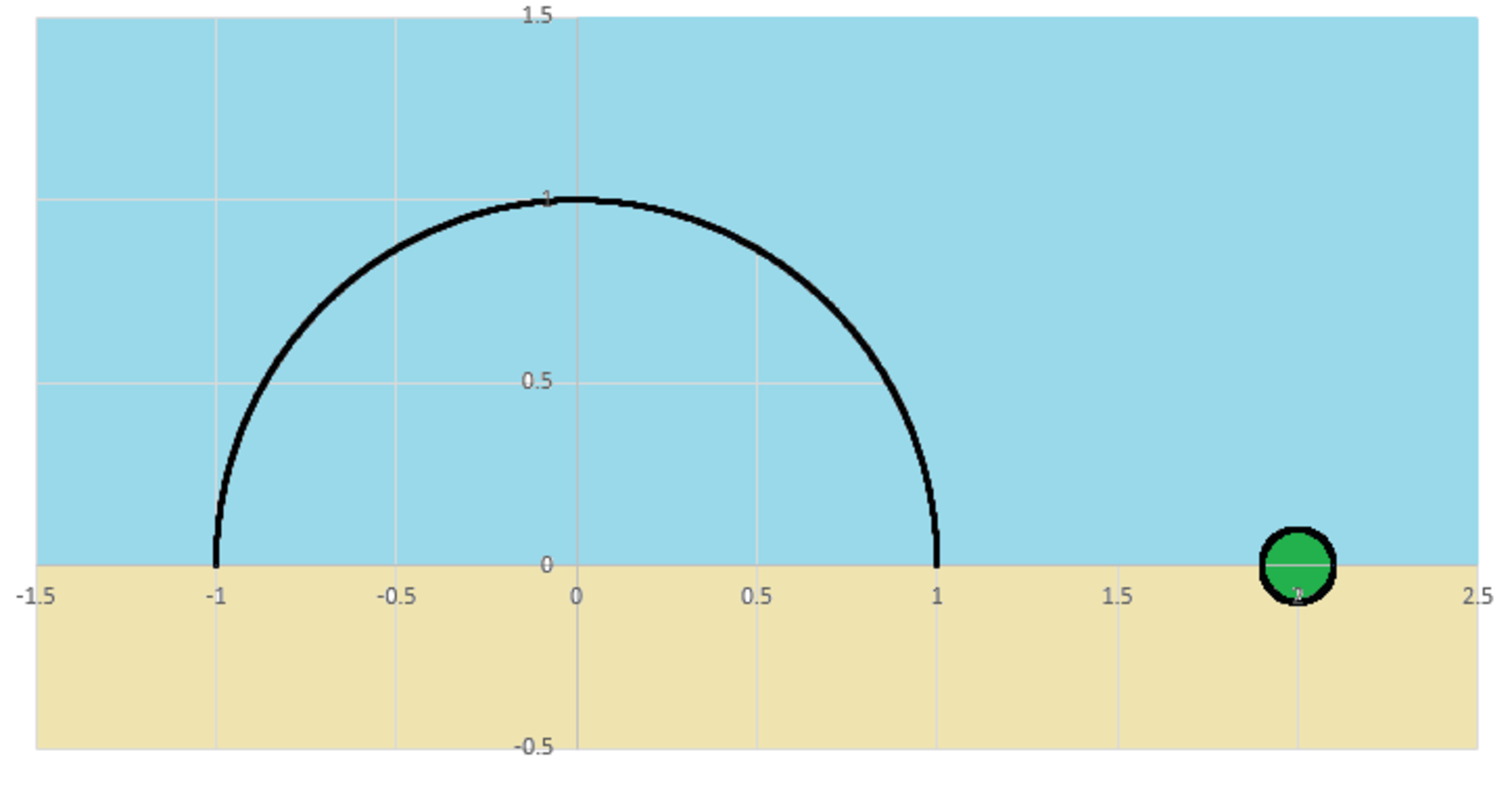
A circular half ring with mass and radius has its center at the origin of the plane. The ring lies in the plane, and it is mounted at its two end points to a flat surface at (shown in a tan color). The mounting supports allow the ring to slide left or right with no resistance, but all other forms of motion are prohibited. The supports can supply vertical forces (either up or down).
The ring is acted on by three forces:
1)
A vertical reaction force
at
2)
A vertical reaction force
at
3)
A gravity force due to a particle of mass
positioned at
. Universal gravitational constant
What is the magnitude of ?
Note: "Vertical" refers to the direction
The answer is 0.15915.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This was fun!
Consider a point on the ring parameterised in polar coordinates with the angular coordinate as t , and the particle's location to be defined as:
r p = ( R cos t , R sin t , 0 ) r c = ( 2 , 0 , 0 )
The gravitational force using Newton's law acting on an elementary arc length of the ring is:
d F = G ( π M d t ) m ( ∣ r c − r p ∣ 3 r c − r p )
The torque due to this force about the origin is:
d T = r p × d F
We are only interested in the Y component of the force and the torque is essentially only about the Z axis. The values of the force along Y and the torque about the Z axis is found after plugging in expressions, simplifying and integrating from 0 to π :
F y = − ∫ 0 π π ( 5 − 4 cos ( t ) ) 2 3 sin ( t ) d t = − 3 π 1 T z = − 2 ∫ 0 π π ( 5 − 4 cos ( t ) ) 2 3 sin ( t ) d t = − 3 π 2
The above integrals can be easily solved by substitution as the numerator is the derivative of a cosine. These steps are left out. Now, applying a vertical force and torque balance about the origin, one gets the following. The vertical reactions are assumed to be along the positive Y direction.
F L + F R + F y = 0 ⟹ F L + F R = 3 π 1 F L R = F R R + T z ⟹ F R − F L = 3 π 2
Adding the above equations followed by halving both sides results in F R = 2 π 1