Half sine

The curve represented by the line through A is $y=A$ . This intersects the curve $y=\sin x$ at: $A=\sin x\\ \therefore x=\sin^{-1}A$ This, of course, only gives the solution of $-\frac{\pi}{2}<x\leq\frac{\pi}{2}$ while we can see from the graph that the lines intersect at a second point on the other side of the hill. However, the graph of $\sin x$ is symmetrical and we can simply split it in half then double it, i.e. $\int_n^{\pi-n}\sin(x)dx=2\int_n^\frac{\pi}{2}\sin(x)dx$ Now we only have to consider the first point. Taking the area under $y=\sin x$ minus the area under $y=A$ as equal to 1: $\begin{aligned}2\int_{\sin^{-1}A}^\frac{\pi}{2}\left(\sin x-A\right)dx&=1\\ 2\Big[-\cos x-Ax\Big]_{\sin^{-1}A}^\frac{\pi}{2}&=1\\ 2\left(-\cos\frac{\pi}{2}-A\frac{\pi}{2}+\cos\sin^{-1}A+A\sin^{-1}A\right)&=1\\ -\pi A+2\sqrt{1-A^2}+2A\sin^{-1}A&=1\end{aligned}$ Since this involves both trigonometric functions and other functions and has no trivial solutions, we cannot easily find a closed-form solution. However, we can still solve this numerically with a calculator such as WolframAlpha , and we get an answer of approximately $\boxed{0.3600349828}$

The area under the curve $y = \sin x$ over a semiperiod is congruent to the area of $y = \cos^{-1} x$ from $0 \leq x \leq 1$ and $-\frac{\pi}{2} \leq y \leq \frac{\pi}{2} \cdot \pi$ , as one is a shift and reflection of the other.

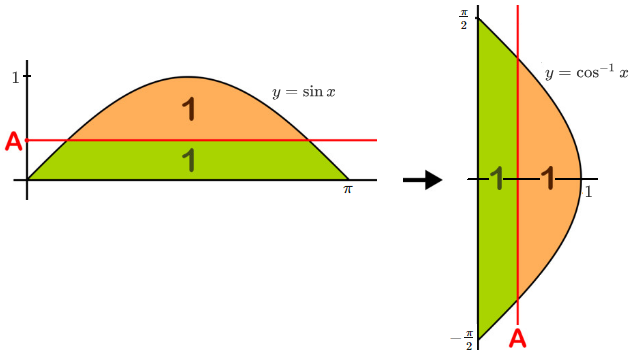
Therefore, the desired horizontal line is now a vertical line and its location can be found by solving:

$2 \int_{0}^{A} \cos^{-1} x dx = 1$

$2[x \cos^{-1} x - \sqrt{1 - x^2}]_0^A = 1$

$2[(A \cos^{-1} A - \sqrt{1 - A^2}) + 1] = 1$

$A \cos^{-1} A - \sqrt{1 - A^2} = -\frac{1}{2}$

which solving numerically gives $A \approx \boxed{0.360035}$ .

There is an $\alpha$ between 0 and $\pi$ such that $(\alpha ; sin \alpha) = (\alpha ; A)$

The top area is $\int_{\alpha}^{\pi-\alpha} sin(x)-sin(\alpha) \, \mathrm{d}x =1$

( $\alpha$ cannot be replaced by the other "intuitive solution" $\pi-\alpha$ because it would give -1 instead of +1.)

Let us not prove, it is visible on the graph, that $\alpha$ between 0 and $\frac{\pi}{2}$ .

By symmetry $\int_{\alpha}^{\pi-\alpha} sin(x) \, \mathrm{d}x = 2\times \int_{\alpha}^{\frac{\pi}{2}} sin(x) \, \mathrm{d}x$

and $\int_{\alpha}^{\pi-\alpha} sin(\alpha) \, \mathrm{d}x = 2\times \int_{\alpha}^{\frac{\pi}{2}} sin(\alpha) \, \mathrm{d}x.$

We look for $\alpha$ such that $2\times\int_{\alpha}^{\frac{\pi}{2}} sin(x) \, \mathrm{d}x = 1 + 2\times sin(\alpha)\times(\frac{\pi}{2}-\alpha$

After integration we look for the root (the $x=\alpha$ such that) $f(x)=2cos(x)-1+2(sin(x))\times(x-\frac{\pi}{2})=0$

I use dichotomy in this Excel sheet to find the solution with 3 decimals - not elegant, but enough for an intuitive physicist to find affordable solution (making lie the physicist Arnold Sommerfield, teacher of Peter Debye, Wolfgang Pauli, Werner Heisenberg, having declared "if you want to be a physicist, you must do three things—first, study mathematics, second, study more mathematics, and third, do the same.")

I got much luck. Forgetting operating sinus, i entered $\alpha$ instead A = sin $\alpha$ ; i.e. 0.368 instead of 0.360 The machine counted me a good answer. :)