Handle a broken forearm
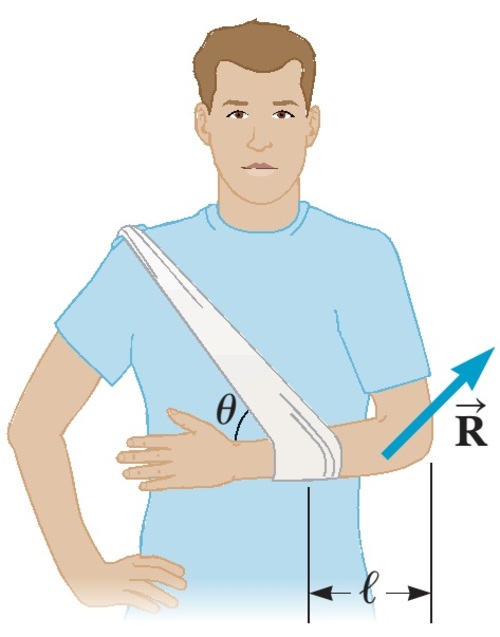In an emergency situation, a person with a broken forearm ties a strap from his
hand to clip on his shoulder . His 1.60-kg forearm remains in a horizontal position and the strap makes an angle of theta = 50.0° with the horizontal. Assume the forearm is uniform, has a length of l = 0.320 m, assume the biceps muscle is relaxed, and ignore the mass and length of the hand.
Find the tension in the strap. Answer is in Newton
The answer is 10.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
T sin(50) = mg /2 Consider his elbow as pivot and the point his strap is attached as other pivot. As it is inclined at an angle 50 deg with the horizontal we will take its component parallel to the vertical. Now as his hand is supported at two points, each point must provide force equal to half of weight of his hand. We won't need the length of his hand, until the concept of torque is used. But that's waste of time.