Handle with care I
If the closed form of m = 1 ∑ ∞ n = 0 ∑ ∞ ( 2 m + n ) 2 ( − 1 ) m = a G − b c π a where a and c are primes. Find the value of a + b + c .
Notation : G is Catalan's constant .
This is an original and modified version of Handle with care II . It would be better to solve problem without integration.
The answer is 37.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Here I wish to share my solution without integration
m
=
1
∑
∞
n
=
0
∑
∞
(
2
m
+
n
)
2
(
−
1
)
m
=
m
=
1
∑
∞
(
−
1
)
m
n
=
0
∑
∞
(
2
m
+
n
)
2
1
if we write the inner sum in series form we notice that
n
=
0
∑
∞
(
2
m
+
n
)
2
1
=
S
1
4
1
n
=
0
∑
∞
(
m
+
n
)
2
1
+
S
2
n
=
1
,
3
,
5
⋯
∑
∞
(
2
m
+
n
)
2
1
and hence have
m
=
1
∑
∞
n
=
0
∑
∞
(
2
m
+
n
)
2
(
−
1
)
m
=
m
=
1
∑
∞
(
−
1
)
m
S
1
4
1
n
=
0
∑
∞
(
m
+
n
)
2
1
+
m
=
1
∑
∞
(
−
1
)
m
S
2
n
=
1
,
3
,
5
⋯
∑
∞
(
2
m
+
n
)
2
1
] we now evaluate the
S
1
and
S
2
separately as follows
4
S
1
=
m
=
1
∑
∞
n
=
0
∑
∞
(
m
+
n
)
2
(
−
1
)
m
=
m
=
1
∑
∞
(
−
1
)
m
(
m
2
1
+
(
m
+
1
)
2
1
)
+
m
=
1
∑
∞
(
−
1
)
m
(
(
m
+
2
)
2
1
+
(
m
+
3
)
2
1
)
+
⋯
=
Telescopes
m
=
1
∑
∞
(
(
m
+
1
)
2
1
−
m
2
1
)
+
Telescopes
m
=
1
∑
∞
(
(
m
+
3
)
2
1
−
(
m
+
2
)
2
1
)
+
⋯
=
−
(
1
2
1
+
3
2
1
+
5
2
1
+
⋯
)
=
−
m
=
1
∑
∞
(
2
m
−
1
)
2
1
=
−
(
m
=
1
∑
∞
m
2
1
−
4
1
m
=
1
∑
∞
m
2
1
)
=
−
8
π
2
therefore we have
S
1
=
−
3
2
π
2
and we are left to evaluate
S
2
=
m
=
1
∑
∞
n
=
1
,
3
,
5
⋯
∑
∞
(
2
m
+
n
)
2
(
−
1
)
m
=
m
=
1
∑
∞
(
−
1
)
m
(
(
2
m
+
1
)
2
1
+
(
2
m
+
3
)
2
1
)
+
m
=
1
∑
∞
(
−
1
)
m
(
(
2
m
+
5
)
2
1
+
(
2
m
+
7
)
2
1
)
+
⋯
=
Telescopes
m
=
1
∑
∞
(
(
2
m
+
3
)
2
1
−
(
2
m
+
1
)
2
1
)
+
Telescopes
m
=
1
∑
∞
(
(
2
m
+
7
)
2
1
−
(
2
m
+
5
)
2
1
)
+
⋯
=
−
(
3
2
1
+
7
2
1
+
1
1
2
1
+
⋯
)
=
−
m
=
0
∑
∞
(
4
m
+
3
)
2
1
=
−
4
2
1
ψ
1
(
4
3
)
=
−
1
6
1
(
π
2
−
8
G
)
or
m
=
0
∑
∞
(
4
m
+
3
)
2
1
=
m
=
1
∑
∞
m
2
1
−
(
m
=
1
∑
∞
(
2
m
)
2
1
+
m
=
1
∑
∞
(
4
m
−
3
)
2
1
)
=
8
π
2
−
(
m
=
0
∑
∞
(
2
m
−
1
)
2
(
−
1
)
m
+
m
=
0
∑
∞
(
4
m
+
3
)
2
1
)
⟹
m
=
0
∑
∞
(
4
m
+
3
)
2
1
=
2
×
8
π
2
−
2
G
thus
m
=
1
∑
∞
n
=
0
∑
∞
(
2
m
+
n
)
2
(
−
1
)
m
=
−
3
2
π
2
+
2
G
−
1
6
π
2
=
2
G
−
3
2
3
π
2
This solution is of Ali Shather
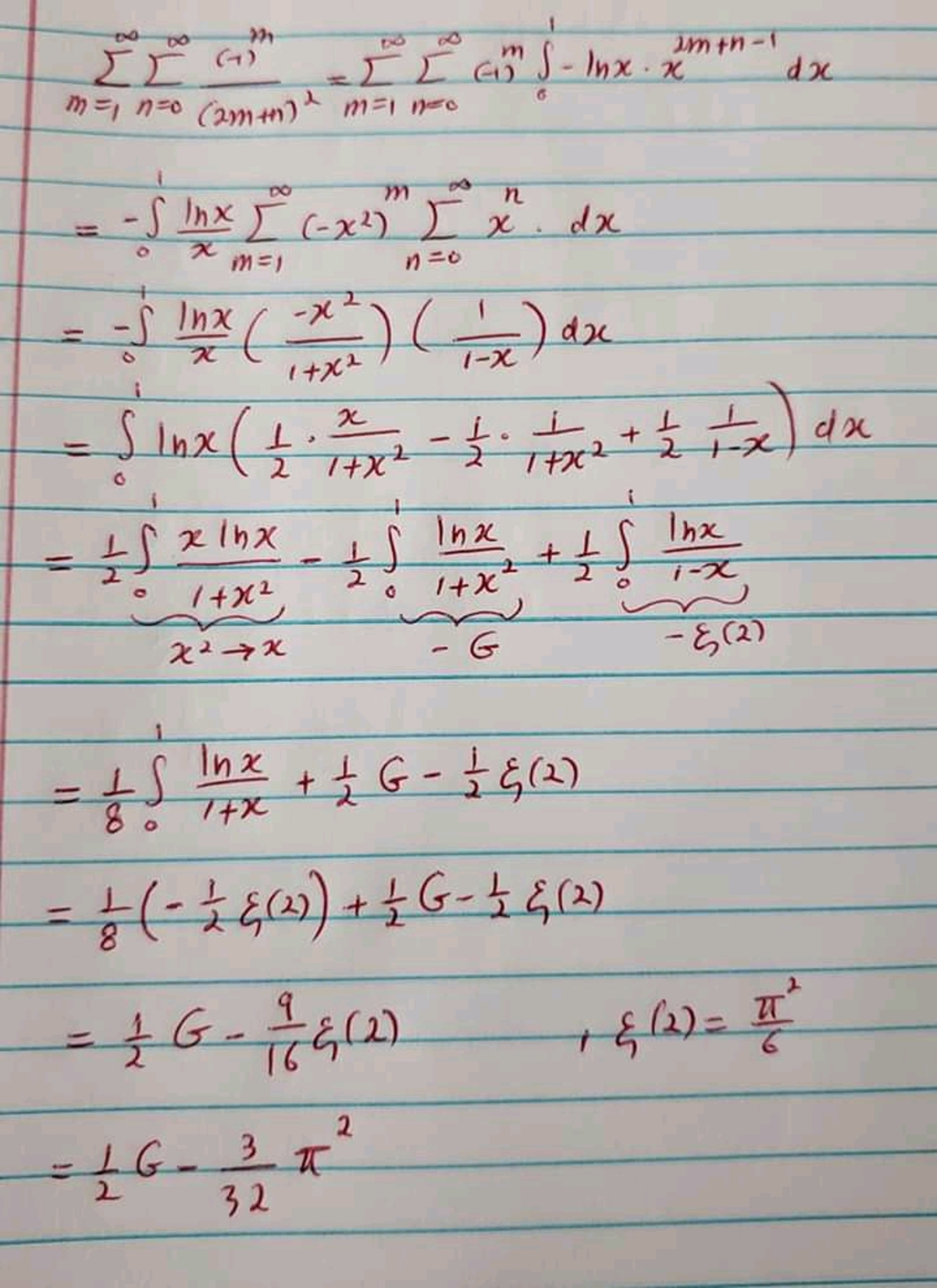
S = m = 1 ∑ ∞ n = 0 ∑ ∞ ( 2 m + n ) 2 ( − 1 ) m = − 2 2 1 − 3 2 1 − 4 2 1 − 5 2 1 − 6 2 1 − 7 2 1 − ⋯ + 4 2 1 + 5 2 1 + 6 2 1 + 7 2 1 + 8 2 1 + 9 2 1 + ⋯ − 6 2 1 − 7 2 1 − 8 2 1 − 9 2 1 − 1 0 2 1 − 1 1 2 1 − ⋯ + ⋯ = − 2 2 1 − 3 2 1 − 6 2 1 − 7 2 1 − 1 0 2 1 − 1 1 2 1 − ⋯ for m = 1 for m = 2 for m = 3
= − ( 2 2 1 + 6 2 1 + 1 0 2 1 + ⋯ ) + ( − 3 2 1 − 7 2 1 − 1 1 2 1 − ⋯ ) = − 2 2 1 ( 1 2 1 + 3 2 1 + 5 2 1 + 7 2 1 + ⋯ ) + 2 1 [ ( 1 2 1 − 3 2 1 + 5 2 1 − ⋯ ) − ( 1 2 1 + 3 2 1 + 5 2 1 + ⋯ ) ] = − 4 1 [ ( 1 2 1 + 2 2 1 + 3 2 1 + ⋯ ) − ( 2 2 1 + 4 2 1 + 6 2 1 + ⋯ ) ] + 2 1 [ G − ( 1 2 1 + 3 2 1 + 5 2 1 + ⋯ ) ] = − 4 1 [ ( 1 2 1 + 2 2 1 + 3 2 1 + ⋯ ) − 2 2 1 ( 1 2 1 + 2 2 1 + 3 2 1 + ⋯ ) ] + 2 1 [ G − ( 1 2 1 + 3 2 1 + 5 2 1 + ⋯ ) ] = − 4 1 [ ζ ( 2 ) − 4 1 ζ ( 2 ) ] + 2 1 [ G − 4 3 ζ ( 2 ) ] = 2 G − 1 6 9 ζ ( 2 ) = 2 G − 3 2 3 π 2 where G denotes the Catalan’s constant. where ζ ( ⋅ ) denotes the Riemann zeta function and ζ ( 2 ) = 6 π 2
Therefore, a + b + c = 2 + 3 2 + 3 = 3 7 .
References: