How Many Digits? A Headache
How many digits does the number 2 1 0 0 0 contain?
You are given that lo g 1 0 2 = 0 . 3 0 1 0 correct up to 4 decimal places.
The answer is 302.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
33 solutions
I had actually gotten this problem wrong, the first two as silly mistakes in my calculation, but the final was correct but I didn't account for an extra digit.
Anyhow! I think my approach to this problem is a lot simpler to everyone else's and I really wish to share it for others to see as well.
So we are all aware that the following is true:
lo g 1 0 2 ≅ 0 . 3 0 1 0 ⟺ 1 0 0 . 3 0 1 0 ≅ 2
Building off this, we can find the amount of digits through doing the following:
( 1 0 0 . 3 0 1 0 ) 1 0 0 0 ≅ ( 2 ) 1 0 0 0
1 0 3 0 1 ≅ 2 1 0 0 0
By observing the left-hand side, we know that 1 0 3 0 1 is just a 1 followed by 301 zeros. Accounting for the 1, the left hand side has 302 digits, so therefore so must the right.
Log in to reply
good solution
The procedure for solving as given by you is very much simpler and useful. Thanks for your upload.
Given L = log₁₀2 is .3010 to 4 decimals, isn't enough information.
Because if that had been .30095 ≤ L < .301, it would round up to .3010, and then the answer would have been 301 digits.
But if it's .301 ≤ L < .30105 (which it is; .3010299957...), it would round down to .3010, making the answer, 302 digits.
Or if you're told that it has been truncated, not rounded, to .3010, which is NOT the usual practice, then you'll get 302 digits.
But without that, the information is insufficient.
Before, note that 1 0 n has n + 1 digits. Taking the common logarithm of 2 1 0 0 0 , l o g 2 1 0 0 0 = 1 0 0 0 l o g 2 = 1 0 0 0 ∗ 0 . 3 0 1 0 3 . . . (Sorry, approximating here) = 3 0 1 . 0 3 . . . Therefore, 2 1 0 0 0 = 1 0 3 0 1 . 0 3 . . . . Since: 1 0 3 0 1 < 1 0 3 0 1 . 0 3 . . . < 1 0 3 0 2 Therefore, the number has 302 digits.
Very good!
same solution :) +1
Yes!
And even more specifically, for non-negative integer n, if 10ⁿ ≤ N < 10ⁿ⁺¹
then N has n+1 digits.
I did it with logs too but it's more fun to think about a solution with no logs. 2^10 is 1024 or 1000X1.024. Therefore 2^1000 = 2^10^100 = (1000X1.024)^100 = (1000^100)X(1.024^100). The least significant figure is 3 decimal spaces to the right... which means every time you multiply it by 1.024 the least significant decimal moves 3 more to the right. We're raising 1.024 to the 100th power which means the least significant figure is 300 spaces to the right. Raising 1.024 to the 100th power on my calculator is 10 plus a fractional remainder. Therefore we have two decimals to the left and 300 to the right... 302!
Using the simple formula to find number if digits in a b = b l o g a + 1
IN THIS CASE, the number of digits in 2 1 0 0 0 = 1 0 0 0 ∗ l o g 1 0 2 + 1 = 1 0 0 0 ∗ 0 . 3 0 1 0 + 1 = 3 0 2
Let 2 1 0 0 0 = 1 0 x then i n t ( x ) + 1 = the number of digits.
1 0 0 0 l o g 2 = x l o g 1 0
x = 1 0 0 0 l o g 1 0 l o g 2
x = 1 0 0 0 l o g 1 0 2
x = 1 0 0 0 × 0 . 3 0 1 0 = 3 0 1 . 0
i n t ( x ) + 1 = 3 0 1 + 1 = 3 0 2
N u m b e r o f D i g i t s i n 2 1 0 0 0 = ⌈ lo g 1 0 2 1 0 0 0 ⌉ = ⌈ 1 0 0 0 ( lo g 1 0 2 ) ⌉ = ⌈ 1 0 0 0 × 0 . 3 0 1 0 2 9 9 ⌉ = ⌈ 3 0 1 . 0 2 ⌉ = 3 0 2
While it gives the correct answer in this instance, it isn't a generally correct way to determine the number of digits in an integer. In particular, it'll be off by one if the number happens to be a power of 10. As such, one should be using ⌊ lo g 1 0 2 1 0 0 0 ⌋ + 1 .
Log in to reply
Agreed. Using a ceiling function would lead to an error in the event that you're finding the number of digits in a power of 10.
NOT A SOLUTION!
BEAUTY OF LOGARITHMS:
Becomes quite simple, if you have a little knowledge of logarithms and understand why such a function evolved. Logarithm is thus one of the most beautiful functions of maths. It not only eases your calculations but also makes big and complicated numbers small ( so as they are readable) and makes very small numbers big enough so that it is easy to handle them, and obviously we can take antilog to get desired result. Moreover, as in this question it tells the number of digits in such a large number.
Beautiful function, isn't it? Love Math, Love Log!!
It was so nerd of you...but I liked...I prefer hyperbolic functions.
Exactly how I did it. :)
2^10 = 1024 (4 digits)
10^x = 2^10
x log 10 = 10 log 2
x = 10 * 0.30103
x = 3.01 ~ 4 digits
2^100 =1267650600228230000000000000000 (31 digits)
10^x = 2^100
x log 10 = 100 log 2
x = 100 * 0.30103
x = 30.103 ~ 31 digits
2^1000 =1267650600228230000000000000000....... (302 digits)
10^x = 2^1000
x log 10 = 1000 log 2
x = 1000 * 0.30103
x = 301.03 ~ 302 digits
Not going to lie. At first I calculated it to be 3011 digits...
total digits= 100Log(2)=301.02999≈302
10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376. Count the number of digits, you will get the answer.Instead you can always use logarithms.
2^n have the number of digits is (3n+1)
where
n is multiple of 10
So, for example, in 2^20 the power contains TWO multiples of 10 so n = 2. Hence there are [3(2) + 1] digits, ie. 7 digits, in the answer. This is clearly true since 2^20 = 1,048,576 !!!
tried this way, I only need to know if this is correct or if there are better ways to solve this:
21000 does not have a factor of 5 obviously therefore we can assume
10m<21000<10m+1 for some m
Assume k=21000, then take log on both sides logk=1000log2≈301.02999>301 Therefore 21000 has 302 digits.
I invite all participants to try thinking in the answer 333 following the idea that number of digits increases 1 each 3-step power of 2 I think that we will move 333 steps to get 332 digits and still remains 2 at last, the last umber multiplied by 2 moves number of digits to 333.
l o g 1 0 2 = 0 . 3 0 1 → 2 = 1 0 0 . 3 0 1
2 1 0 0 0 = ( 1 0 0 . 3 0 1 ) 1 0 0 0 = 1 0 3 0 1
1 0 3 0 1 is 1 followed by 3 0 1 0 's
3 0 1 + 1 = 3 0 2 digits
Given that l o g 1 0 2 ≈ 0 . 3 0 1 0 , we can show that 2 ≈ 1 0 0 . 3 0 1 0 using the definition of a logarithm. So now we have ( 1 0 0 . 3 0 1 0 ) 1 0 0 0 , which is equivalent to 1 0 3 0 1 . 0 , which has 302 decimal places.
Given that log(10) 2≈0.3010, we can rewrite
this as 10^(301/1000)≈2. Since we are
attempting to find the number of digits in
2^1000, we can simply use the property of
substitution and obtain
10^((301/1000)×1000). The 1000's cancel
each other and we are left with 10^301. Now
at this point we may find that the total
number of digits in 10^301 is 302 because the
number of digits in 10^n is n+1. And since
10^301≈2^1000, we may conclude that the
number of digits in 2^1000 is 302. Thus we
obtain 302 as our final answer.
Bash shell one-liner:
1 |
|
and you get 302.
We have 2 1 0 0 0 = 1 0 lo g 1 0 2 1 0 0 0 = 1 0 1 0 0 0 lo g 1 0 2
And using lo g 1 0 2 ≈ 0 . 3 0 1 0 , we have
2 1 0 0 0 = 1 0 1 0 0 0 lo g 1 0 2 ≈ 1 0 0 . 3 0 1 0 ∗ 1 0 0 0 = 1 0 3 0 1
Then, 2 1 0 0 0 is approximately equal to (greater than) 1 0 3 0 1 , which have 3 0 2 digits. And 2 1 0 0 0 = 1 0 1 0 0 0 lo g 1 0 2 is less than 1 0 3 0 2 , which have 3 0 3 digits. It is easy to see that 1 0 1 0 0 0 lo g 1 0 2 = 2 1 0 0 0 is nearer from 1 0 3 0 1 than from 1 0 3 0 2 , and therefore 2 1 0 0 0 must have 3 0 2 digits, and not 3 0 3 .
Given the logarithm: 10^(0.3010) = 2
hence: 2^1000 = 10^301 = 100000000.......... (301 zeros)
hence : the number of digits is 302
2^1000 1000(log2)=301.3 When u take antilog , the characteristic is 302 ... Therefore it would be of the order 10^302 .. So it has 302 digits ..
We can let 2 1 0 0 0 = k, so l o g 2 k = 1000. Then, change the base, l o g 1 0 2 l o g 1 0 k =1000. Given l o g 1 0 2 =0.3010, so l o g 1 0 k =301. Change to index form, k = 1 0 3 0 1 . In this way, we know that there are 302 digits for this value.
Log10 (2^1000) =1000*Log10(2) =1000 * .301=301 So, 10^301 = 2^1000 And 10^n contains n+1 digits So, we get 301+1=302 digits
X=2^1000, LogX=1000Log2 where Log is in base 10.. LogX=1000×0.3010 (Given fact in the problem) LogX=301 X =10^301 The digits in 10^n term are n+1... Hence the number of digits in the answer are 302
2^n contains x+1 digits, where x = floor(n*log2)
(\log_10 2\ )= x
10^{x} = 2
if x = 0.3010
10^{0.3010} = 2
We know that log2=0.301. So, 10^0.301=2. So 2^1000=10^301. 10^301 has 302 digits, so the answer is 302 digits. (P.S. 10^301 is not equal to 2^1000, it's an approximation due to an approximate logarithmic value)
Given that log 2 = 0.3010
log 2 ^ 1000 = 1000 log 2 = 1000 (0.3010) = 301
2 ^ 1000 = 10 ^ 301
2 ^ 1000 contains 302 digits.
log 2 1 0 0 0 = 1000log 2 = 301.0299957 ≃ 302
2^1000 is not a multiple of 10 therefore: 10^x < 2^1000 < 10^(x + 1) 10^x = 2^1000 xlog10 = 1000log2 x = 301.3 therefore 2^1000 is between 10^301 and 10^302 Therefore it has 302 Digits.
2^1000 = x . Taking Log on both sides :- 1000 log 2 = log x
1000 (.3010) = log x
301 = log x Taking antilog :- 10^301 = x
Since , raising 10 to any power gives a number having number of digits (1+value of power raised ). So x = 2^1000 will have 301+1=302 digits :)
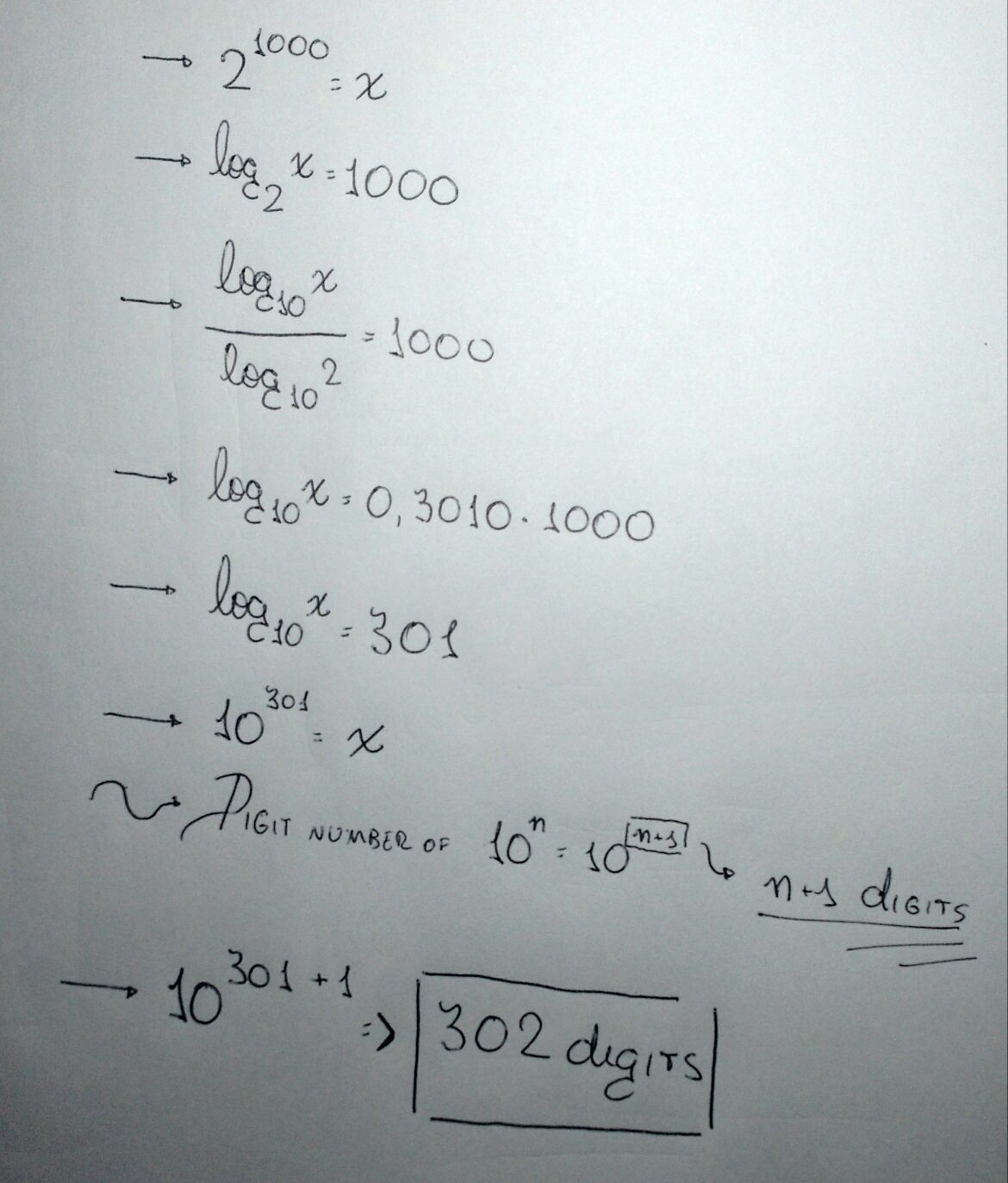
As 2 1 0 0 0 is not a multiple of 10, it follows that 1 0 m < 2 1 0 0 0 < 1 0 m + 1 , where 1 0 m and thus 2 1 0 0 0 contain m + 1 digits.
Since 1 0 0 0 lo g 2 ≈ 3 0 1 . 0 2 9 9 9 , m = ⌊ 3 0 1 . 0 2 9 9 9 ⌋ = 3 0 1 , so 2 1 0 0 0 contains 302 digits.