Hanged bird feeder
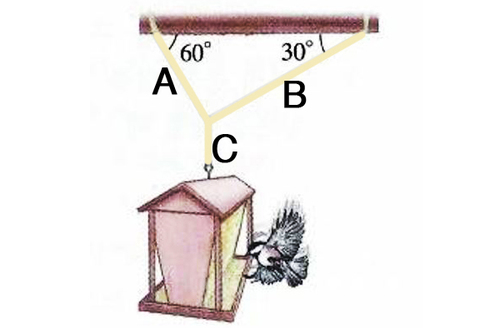 The above diagram shows a bird feeder hanging from the ceiling by three wires
and
Wires
and
form angles of
and
respectively, with the ceiling. Wire
is hanging from the intersection of
and
and is connected to the top of the bird feeder. If the weight of the feeder is
what is the tension force on the wire
The above diagram shows a bird feeder hanging from the ceiling by three wires
and
Wires
and
form angles of
and
respectively, with the ceiling. Wire
is hanging from the intersection of
and
and is connected to the top of the bird feeder. If the weight of the feeder is
what is the tension force on the wire
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let T A and T B be the tensions in wire A and B respectively. Then equating the horizontal forces: T A c o s 6 0 ∘ = T B c o s 3 0 ∘ ⇒ T A = 3 T B Now equating vertical forces, we have: T A s i n 6 0 ∘ + T B s i n 3 0 ∘ = 6 5 ⇒ 2 3 T A + 2 1 T B = 6 5 ⇒ 2 3 T B + 2 1 T B = 6 5 ⇒ 2 T B = 6 5 ⇒ T B = 3 2 . 5 N