Hanging Out to Dry
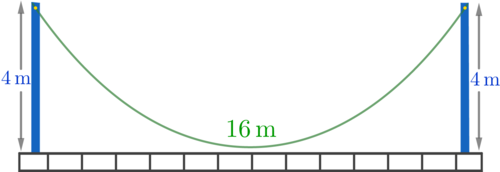
A 1 6 m cable is suspended from the tips of two poles of equal heights 4 m .
What should be the minimum separation between the poles so that the cable doesn't touch the ground?
The answer is α ln β for integers α and β where β is a prime number. Find α + β .
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
A suspended cable hangs in a catenary , and if we let the ground be the x -axis, then a catenary with the minimum separation between the poles will be one that passes through the origin at its axis of symmetry, which follows the equation y = a cosh ( a x ) − a , with an arc length of s = 2 a sinh ( a x ) .
The first equation can be rearranged to cosh ( a x ) = a y + a and the second to sinh ( a x ) = 2 a s . Then using the identity cosh 2 ( t ) − sinh 2 ( t ) = 1 , we have ( a y + a ) 2 − ( 2 a s ) 2 = 1 , and since y = 4 when s = 1 6 , we have ( a 4 + a ) 2 − ( 2 a 1 6 ) 2 = 1 , and solving this gives us a = 6 . So the equation of the catenary is y = 6 cosh ( 6 x ) − 6 .
We want to find the separation along the ground, which is 2 x when y = 4 . So 4 = 6 cosh ( 6 x ) − 6 , and since cosh t = 2 1 ( e t + e − t ) , our equation becomes 4 = 6 ⋅ 2 1 ( e 6 x + e − 6 x ) − 6 , which solves to x = 6 ln 3 . This means the separation along the ground is 2 x = 2 ⋅ 6 ln 3 = 1 2 ln 3 , and so α = 1 2 and β = 3 , and α + β = 1 2 + 3 = 1 5 .
The cable hangs in a catenary y = a cosh a x − X ≤ x ≤ X for some a , X > 0 . Thus d x d y = sinh a x d x d s = cosh a x and so the length of the cable is 1 6 = ∫ − X X cosh a x d x = 2 a sinh a X = 4 a sinh 2 a X cosh 2 a X If the centre of the cable just brushes the ground, then 4 = a ( cosh a X − 1 ) = 2 a sinh 2 2 a X These two equations tell us that tanh 2 a X = 2 1 , so that X = a ln 3 . Thus sinh a X = 3 4 , and hence a = 8 c o s e c h a X = 6 . Thus we deduce that X = 6 ln 3 , and hence the separation of the poles is 1 2 ln 3 .
If the poles were further apart, the cable would hang higher. Thus the answer is 1 2 + 3 = 1 5 .
Let l be the length of the cable, b be the separation between the poles, h be the height of the poles.
Shape of a hanging cable (known as Catenary ) is given by f ( x ) = a cosh ( a x )
Equation of a hanging cable that is tangent to the x -axis (ground) is f ( x ) = a cosh ( a x ) − a
Since the graph is symmetric about y -axis
Arc length of the curve from x = 0 to x = 2 b is ∫ 0 2 b 1 + ( d x d ( a cosh ( a x ) − a ) ) 2 d x = 2 l
Solving the integral and rearranging terms gives ⟹ sinh ( 2 a b ) = 2 a l
Also, h = f ( 2 b ) = a cosh ( 2 a b ) − a
Rearranging the terms gives ⟹ cosh ( 2 a b ) = a h + a
Solving the red and blue simultaneous equations ⟹ b = 4 h l 2 − 4 h 2 ln ( l − 2 h l + 2 h )
Putting l = 1 6 and h = 4 ⟹ b = 1 2 ln 3