Hanging Potted Plant
You want to hang a potted plant 1 0 0 cm from the ceiling held up by three strings attached to hooks in the ceiling. If the hooks are located at points ( 2 0 cm , 1 0 cm ) , ( − 1 0 cm , − 1 0 cm ) , ( 1 0 cm , − 1 0 cm ) , can you hang the potted plant at a position 1 0 0 cm vertically below the point ( 0 cm , 0 cm ) in the ceiling?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
See @Timothy Watson for a geometrical interpretation. Here's an algebraic interpretation. Let v 1 , v 2 , v 3 be vectors from the pot to the anchor points. Let T 1 ′ , T 2 ′ , T 3 ′ be the force multipliers for the strings (they are not the actual tensions because v 1 , v 2 , v 3 are not unit vectors) . The force balance equations for the pot are (where W is the pot weight).
T 1 ′ v 1 x + T 2 ′ v 2 x + T 3 ′ v 3 x = 0 T 1 ′ v 1 y + T 2 ′ v 2 y + T 3 ′ v 3 y = 0 T 1 ′ v 1 z + T 2 ′ v 2 z + T 3 ′ v 3 z = W
For positive weight W , the force multipliers must all be positive, since a string can only pull, and cannot push. Solve the system for W = 1 0 0 by inverting the system matrix and pre-multiplying by the vector of forces. In this case, one of the tensions is negative, indicating that the arrangement is non-physical.

If we look at the problem from the top-down perspective, we can mark the location of each hook. Drawing lines connecting each dot we create a triangle, and we can clearly see that the origin does not lie within the triangle that we have created.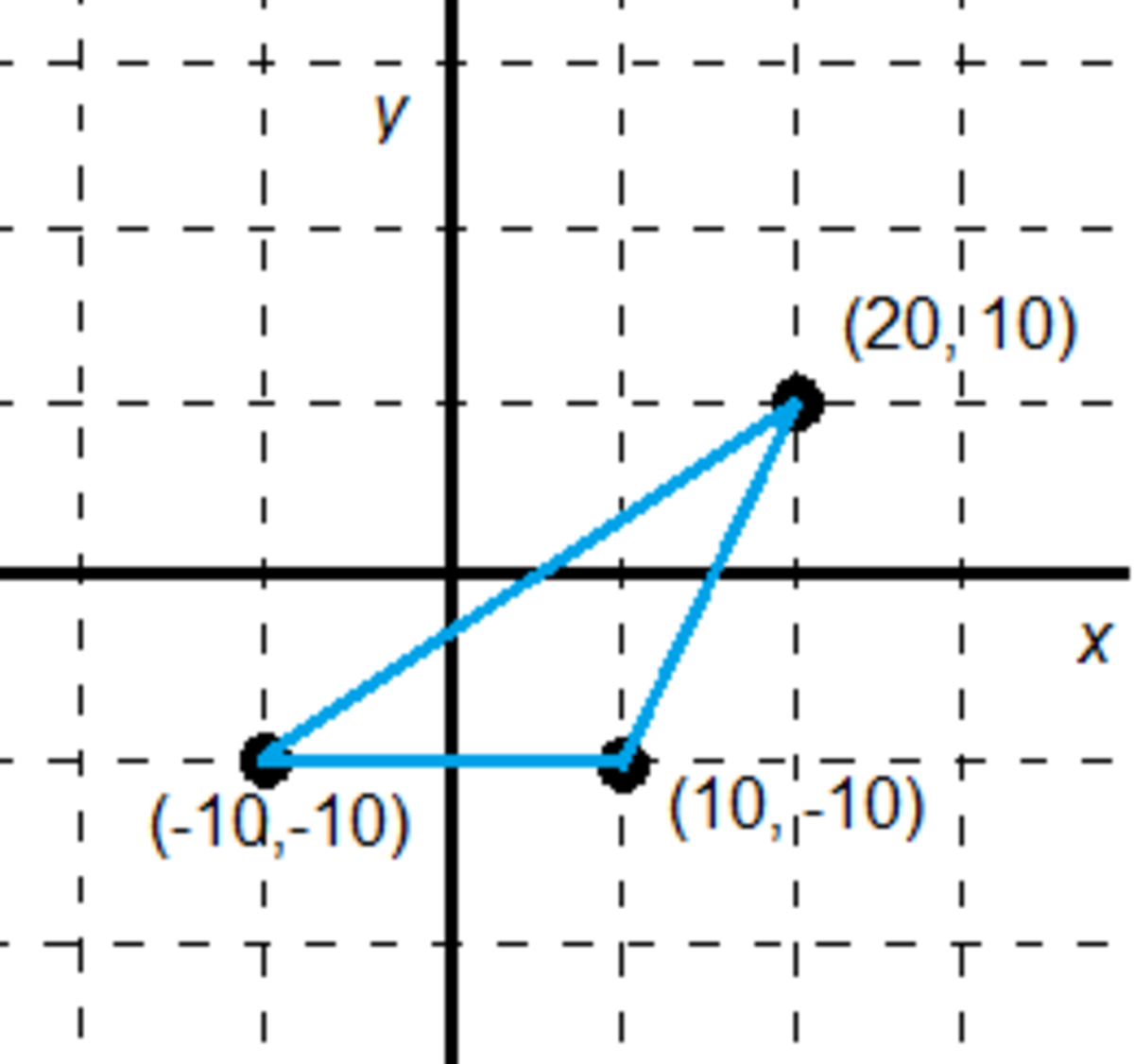 If we were to hang anything from these three hooks, we could vary the tensions in the strings to support the object at any point inside the triangle. However, we cannot hang anything outside the triangle since the strings can only pull the plant towards the hooks, not push it away.
If we were to hang anything from these three hooks, we could vary the tensions in the strings to support the object at any point inside the triangle. However, we cannot hang anything outside the triangle since the strings can only pull the plant towards the hooks, not push it away.