Hanging Spheres
As shown in the diagram, spheres A and B are hanging from the corners of the ceiling, and are connected with a string. The centers of spheres A and B are distances d A and d B apart from their respective walls.
What can we say about the respective masses M A and M B of the spheres based on the distances d A and d B ?
Assume that the system is in equilibrium, that the string joining the masses is taut and horizontal, that the spheres are the same size, and that d B > d A .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
My understanding of trigonometry and trigonometric operations prevent me from understanding the equations.
I only got A from intuition, thinking of push-pull practice in real life.
Thank u ...I understand it now...
What if you were not allowed to assume 'h' was the same for both balls? Would you still have been able to solve the problem in a similar way?
(After all, in the original diagram, the left ball is actually attached to the wall, not the ceiling, and although I think its tiny difference in distance totally justifies your approximation that 'h' is the same in this particular scenario, I still wonder how much it would complicate your solution if you were faced with a similar scenario in which everything was the same except that the difference in height 'h' was quite significant between the two balls, for example because the left ball's string was attached much farther down the wall).
Suppose that the tensions in the slanting strings are T A , T B , and that the tension in the horizontal string is T . Suppose also that the slanting strings make angles θ A , θ B with the horizontal. Since particle A is in equilibrium, resolving forces horizontally and vertically gives T = T A cos θ A m A g = T A sin θ A Dividing these two equations gives m A = g T tan θ A Similarly, we obtain m B = g T tan θ B Since d A < d B we have tan θ A > tan θ B , and hence m A > m B .
Where are we told that dA < dB? Just because it appears to be so in the diagram is no justification. The problem is unanswerable.
Log in to reply
the assumption was stated at the end of the question.
Log in to reply
True, but it was not stated to begin with. The angles of the strings made things fairly clear, though.
Sir I had a doubt that why did u do T=Tcos theta
Log in to reply
The horizontal component of the tension T A is T A cos θ A , which must match the horizontal tension T .
It should be weight, because mass is the material present in a body
Log in to reply
If they are in uniform gravitational field, then weight is proportional to mass.
Log in to reply
yes, weight is proportional to mass, but mass is constant quantity everywhere in the universe, the weight of a body changes according to external forces applied, for example if the weight of a body is 60 kg on earth then it will become 10 kg on the moon but mass of that body remains the same on earth as well as on moon.
Just a simple question: If the string between them is taught and horizontal , then the masses must be the same, correct? In other words, if mass A was greater, then it would continue towards the left/down, pulling ball B up until the string connecting A and B was in-line with the string connecting the wall and B. I based my answer on this simple assumption. Am I wrong?
Log in to reply
You are wrong, I am afraid. Read the details of the given solutions.
It would be impossible for the two strings attached to B to be in a non-vertical straight line, since B could never be in equilibrium like that. The actual position for equilibrium depends on the actual lengths of the joining strings.
- Since the balls are at rest, the horizontal component of tension in the leftmost string must equal the horizontal component of tension in the rightmost string.
- This implies that vertical component of the tension in the leftmost string is d b / d a times the vertical component of tension in the rightmost string.
- This implies the ratio of the weight of ball A to the weight of ball B is d b / d a .
Proof of 1: The balls are not accelerating so net horizontal force acting on them is zero.
Proof of 2: Follows from considering a right triangle with sides formed by the leftmost string, the left wall and a horizontal line connecting the center of a A to the left wall. Similarly consider also a triangle formed by the rightmost string, the right wall and a horizontal line connecting the center of B to the right wall. The tensions of the leftmost and rightmost strings, together with their horizontal and vertical components form triangles similar to the triangles just described. Together with statement #1, this implies statement #2.
Proof of 3: Follows from #2 and the fact that the weight of ball A equals the vertical tension in the leftmost string and the weight of ball B equals the vertical tension in the rightmost string.
shouldn't the string in the middle be tilted so that B is higher than A because A is heavier?
Imagine you are holding both spheres, and have equal mass, if you release them, they will tend to go to the center, wich is different from the diagram, hence the ball A is heavier
Intuitively, if B were heavier than it is, then it would sink lower and cause the string A-B would tilt down to the right (no longer be horizontal). Also, adding weight to B would pull A further away from the left wall.
If weight were added to A, likewise B would be pulled further away from the right wall.
If A and B were equal in weight, and the corner mounted strings were the same length, then the string A-B would be horizontal. Increasing the length of the right corner-to-B string (as is the case in the diagram) would cause B to sink lower.
So we can see that a higher mass OR a longer string makes the ball sink lower. So if B has a longer string, then it must weigh less to compensate (and keep the connecting string horizontal).
Horizontal tension is constant because there are no horizontal forces excepts at the extremes of the rope. The vertical tension is equal to the weight of each mass, being the tract AB horizontal.
m B m A = N B N A = tan ( α B ) tan ( α A ) > 1
What does distance say about mass? Or how do they correlate? More energy is needed to propel more mass. So it's more likely that B would go further only if it weighed less than A which only traveled a smaller distance.
If you have to lift a ball on a string, like you are pushing a kid on a swing set, up past the point of equilibrium, that takes work. If you have to push the ball higher it takes even more work. As you can see from the diagram, B is "lifted higher" than A, which takes more work. So, if the balls are in equilibrium, yet evenly balanced, A must be doing more work than B, because it is harder to hold up B than it is A. So A is more massive.
Had it been Ma =Mb ,the combined cg would have been at centre but since da<db => cg towards Ma(for combined system of mass) => Ma>Mb
Let's take the case when D A = D B. By symmetry we can say that M A = M B. Now if we increase the mass of A, A goes down making the AB line slant. To make AB line horizontal, we have to pull the string connecting A to the wall. This makes D A < D B. Thus we obtain the case given in the question.
The moment of inertia of a sphere (I) = 3 2 M R 2
A and B are identical. (Given)
I observe that since they are in equilibrium, the net torque (T) = 0.
T A = T B
⟹ I A . α A = I B . α B
⟹ 3 2 M A R 2 . d A a = 3 2 M B R 2 . d B a
⟹ M B M A = d B d A
Thus, if d A < d B , then M A < M B
The potential energy of B is greater than A adding to the mass of B.
Log in to reply
It's in equilibrium. PE should be the same. B took a greater distance thus lighter
This is not a correct approach. B has been pulled higher relative to its own equilibrium than A, thus A needs to be heavier. You'll see this when you draw the force vectors.
Log in to reply
M(a)>M(b) as tangent of the angle subtended by sphere (b) with the wall is Greator than what subtended by other sphere.
Ma should be greater than Mb
This makes no sense.
There is no torque about the center of the spheres. They are connected through their centers.
Use the following diagram as a guide: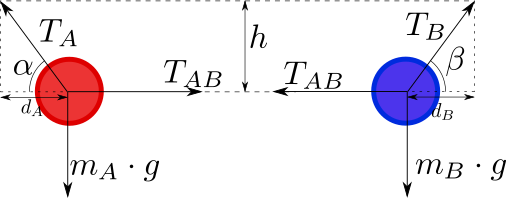 h
stands for the height at which
A
and
B
are suspended (the middle string is horizontal, so it's the same for both).
T
A
B
is the tension in the string between
A
and
B
(same for both) and
T
A
and
T
B
are the tensions on the strings pulling diagonally upwards with angle
α
and
β
on
A
and
B
respectively.
The balls are in equilibrium, so the net force acting on each one of them must be zero. In particular, we can decompose the horizontal and vertical components of each ball:
h
stands for the height at which
A
and
B
are suspended (the middle string is horizontal, so it's the same for both).
T
A
B
is the tension in the string between
A
and
B
(same for both) and
T
A
and
T
B
are the tensions on the strings pulling diagonally upwards with angle
α
and
β
on
A
and
B
respectively.
The balls are in equilibrium, so the net force acting on each one of them must be zero. In particular, we can decompose the horizontal and vertical components of each ball:
By solving for T A B on equations 2 and 4, we get the following new equation:
T A cos α = T B cos β
And by solving for g on equations 1 and 3 we get the following one:
m A T A sin α = m B T B sin β
Now we can solve for T B on the first new equation to get the following substitution:
T B = cos β T A cos α
And we can use this substitution on the other equation:
m A T A sin α = m B cos β T A cos α sin β = cos β m B T A cos α sin β
In the previous expression we can cancel out T A on both sides and rearrange the rest as so:
m A m B = sin α cos α ⋅ cos β sin β = tan α tan β
The tangent of α and β can be obtained from the two right triangles on each side, having in mind that tan θ = a d j a c e n t o p p o s i t e :
tan α = d A h
tan β = d B h
By substitution in the previous equation we get:
m A m B = tan α tan β = h / d A h / d B = d B d A
What we get from this last equation, namely m A m B = d B d A , is that the mass of a ball is inversely proportional to its distance to the wall. Thus, the ball closer to the wall (in this case A ) will have a bigger mass.
m A > m B