Happy diamond
What is the area of a rhombus of side 13 such that the sum of its two diagonals is 34?
The answer is 120.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
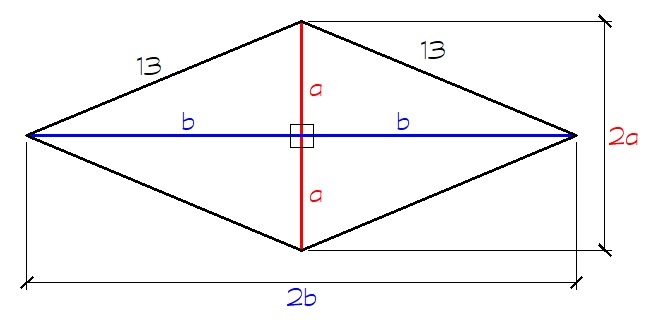 Consider the diagram. From the problem,
2
a
+
2
b
=
3
4
or
a
+
b
=
1
7
or
a
=
1
7
−
b
.
By pythagorean theorem, we have
Consider the diagram. From the problem,
2
a
+
2
b
=
3
4
or
a
+
b
=
1
7
or
a
=
1
7
−
b
.
By pythagorean theorem, we have
1 3 2 = a 2 + b 2
1 6 9 = ( 1 7 − b ) 2 + b 2
b 2 − 1 7 b + 6 0 = 0
b − 5 = 0 ⟹ b = 5
b − 1 2 = 0 ⟹ b = 1 2
Based form the diagram, b > a , therefore b = 1 2 and a = 5 . It follows that 2 a = 2 ( 5 ) = 1 0 and 2 b = 2 ( 1 2 ) = 2 4 .
The area of a rhombus is half the product of its diagonals. Therefore
A = 2 1 ( 2 a ) ( 2 b ) = 2 1 ( 1 0 ) ( 2 4 ) = 1 2 0
This is my own solution using my old account. I have a new account now.
Una solución fácil y rápida es buscar una terna pitagórica con C=13, la cual seria 5^2 + 12^2=13^2, 5 y 12 serian la mitad de las diagonales, asi que las multiplicamos X2, ya solo nos queda aplicar la formula (Dxd/2)(24x10/2)=120
Let a and b be the diagonals of rhombus.
Thus, A r e a = 2 a b , so we need to manipulate the value of 2 a b
We know that 4 s 2 = a 2 + b 2 and a + b = 3 4 , and we have s = 1 3
Since a 2 + b 2 = ( a + b ) 2 − 2 a b
So 4 s 2 = ( a + b ) 2 − 2 a b
Substitute all the given values to get,
4 × 1 3 2 = 3 4 2 − 2 a b
2 a b = 1 2 0
it's simple with picture so that you can save this..... :-)
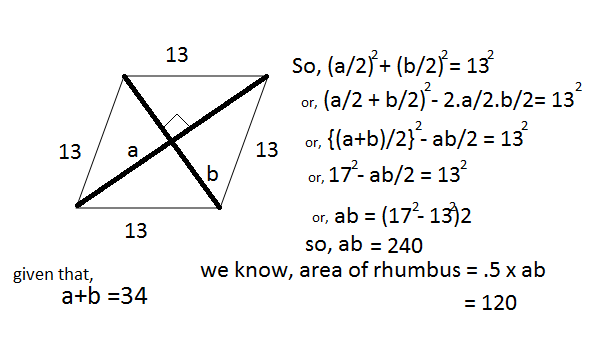
are you using parallelogram law?
Log in to reply
no,,it's Pythagorean law......and the diagonals of a rhombus bisect themselves equally in right angle.
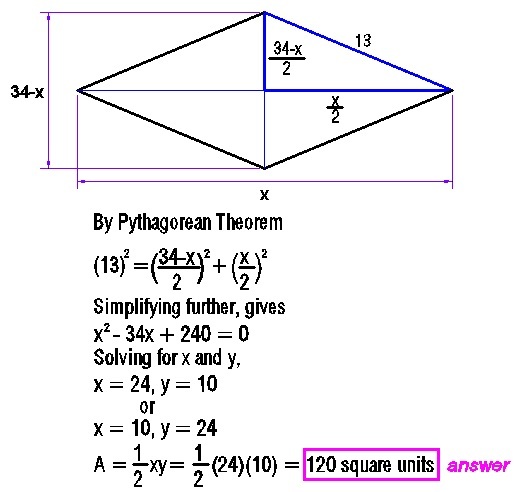
Solution 1:
By Pythagorean theorem a 2 + b 2 = 1 3 2 and the problem 2 ( a + b ) = 3 4 , so 2 a b = ( a + b ) 2 − ( a 2 + b 2 ) = 1 7 2 − 1 3 2 = 1 2 0 where a b = 6 0 . ∴ rhombus area is 4 2 a b = 4 ( 3 0 ) = 1 2 0
Solution 2:
Also we can get diagonal length by Pythagorean theorem. Make b = 1 7 − a then ( 1 7 − a ) 2 + a 2 = 1 3 2 ⇒ 6 0 − 1 7 a + a 2 = ( a − 1 2 ) ( a − 5 ) = 0 so a = 1 2 , 5 and b = 5 , 1 2 respectively. ∴ rhombus area is 2 2 a × 2 b = 2 1 0 × 2 4 0 = 1 2 0