Happy New Year 2016
Let x , y , z be positive reals such that x 2 + y 2 + z 2 = 1 if a x y + b y z = 2 a 2 + b 2 for some positive real numbers a and b , then the value of y can be expressed as
B C A
where A and B are co-prime positive integers and a square free natural number C . Find A + B + C .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
By the arithmetic-geometric inequality of absolute happiness,
2 x 2 + a 2 + b 2 a 2 y 2 + 2 a 2 + b 2 b 2 y 2 + z 2 ≥ a 2 + b 2 a 2 x 2 y 2 + a 2 + b 2 b 2 z 2 y 2
Which results in
2 a 2 + b 2 ≥ a x y + b y z
wherein equality is achieved if and only if a 2 + b 2 a 2 y 2 = x 2 and a 2 + b 2 b 2 y 2 = z 2
Now, with more happiness, we substitute these into the equation
x 2 + y 2 + z 2 = 1
a 2 + b 2 a 2 y 2 + y 2 + a 2 + b 2 b 2 y 2 = 1
2 y 2 = 1 , y = 2 1
Now, after repeatedly doubting the answer which you have derived because it doesn't seem to fit the answer format (why does the answer format have to be like that???) we get A=1, B=1, C=2 ( y = 1 2 1 )
Then, A + B + C = 4
similar way!
using the c-s inequity: y 2 ( a 2 + b 2 ) ( x 2 + z 2 ) ≥ ( a x y + b z y ) 2 ( a x y + b y z ) ≤ y 2 ( a 2 + b 2 ) ( 1 − y 2 ) = ( a 2 + b 2 ) ( y 2 − y 4 ) = ( a 2 + b 2 ) ( − ( y 2 − . 5 ) + ( . 5 ) 2 ) we know from a square≥0, or − ( y 2 − . 5 ) 2 ≤ 0 or − ( y 2 − . 5 ) 2 + . 2 5 ≤ . 2 5 . equity occurs at y 2 = . 5 ⟹ y = 1 2 1 . we put the max in a x y + b y z ≤ ( a 2 + b 2 ) ( y 2 − y 4 ) ≤ ( a 2 + b 2 ) . 2 5 = 2 a 2 + b 2 so y must be that value or else the equity cant be achieved.
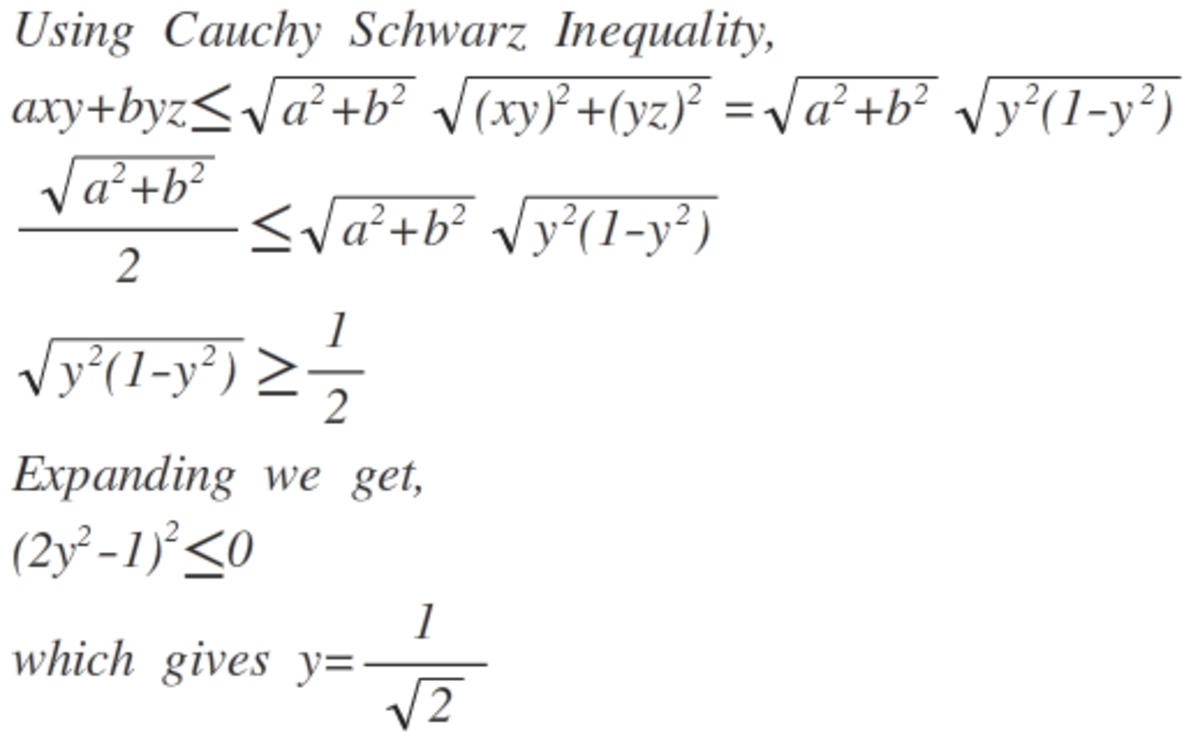
Let
y = sin θ
x = cos θ sin α
z = cos θ cos α
∴ a x y + b y z = sin θ cos θ × ( a sin α + b cos α )
∴ a x y + b y z = 2 a 2 + b 2 sin 2 θ × sin ( α + β ) where β = arccos ( a 2 + b 2 a )
This value is equal to 2 a 2 + b 2 when α + β = 2 π
& 2 θ = 2 π → θ = 4 π
∴ y = sin 4 π = 2 1
Comparing, A = 1, B = 1, C = 2.
A + B + C = 1 + 1 + 2 = 4