happy number

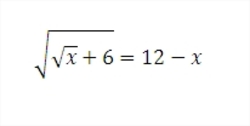
We start by analyzing in which range $x$ must be:

We observe that $x$ has to be $0$ or greater in order to avoid the square root of a negative number. Furthermore, $x$ has to be less or equal to $12$ because, if $x$ was greater than $12$ , the term $12-x$ would be negative, but, since $12-x$ is equal to $\sqrt{\sqrt{x}+6}$ and a square root has to be positive, this can‘t be the case. So we conclude: $0 \leq x \leq 12$

Now we start rearranging the terms of the equation and square both sides: $(\sqrt{\sqrt{x}+6})^2=(12-x)^2$

$\sqrt{x}+6=144-24x+x^2$

$x^2-24x+138-\sqrt{x}=0$

Since $x$ is at maximum $12$ , $\sqrt{x}$ is at maximum $\sqrt{12}$ , which is fairly negligible. We just remove it from our equation and solve for $x$ . But, as we‘ve removed a part, it isn‘t exact anymore but only an approximation: $x_{1,2}=-\frac{-24}{2}\pm\sqrt{(\frac{-24}{2})^2-138}$

$x_{1,2}=12\pm\sqrt{6}$

We can now observe that only one solution is possible because $12+\sqrt{6}$ is greater than $12$ but $x$ has to be less or equal to $12$ . Hence:

$x=12-\sqrt{6}=9.55...$

We plug $12-\sqrt{6}$ into the original equation:

$\sqrt{\sqrt{12-\sqrt{6}}+6}=12-(12-\sqrt{6})$

$\sqrt{\sqrt{12-\sqrt{6}}+6}=\sqrt{6}$

$3.015...=2.449...$

This is obviously wrong, but we can correct that. If we choose a smaller value for $x$ , the left side of the equation gets smaller and the right side gets greater. That way, both sides will meet at one value and the equation will turn valid. Since integer solutions are very popular, we check if the nearest integer below $9.55...$ works, in this case $9$ :

$\sqrt{\sqrt{9}+6}=12-x$

$3=3$

We were lucky, as our equation is now valid and therefore: $\boxed{x=9}$