Happy Victory Day, Vietnam!
Find 1 9 7 5 ! f ( 1 9 7 5 ) ( 0 ) for f ( x ) = ( 1 − x ) 4 ( x + 1 ) x .
Clarifications :
- f ( k ) ( x ) denotes the k th derivative of f ( x ) .
- ! denotes the factorial notation. For example, 8 ! = 1 × 2 × 3 × ⋯ × 8 .
The answer is 2569862100.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
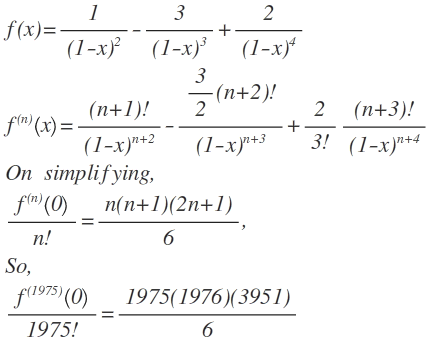
Yes, exactly! (+1) Note that the answer is ∑ k = 1 1 9 7 5 k 2 . In fact, this is one way to derive the formula ∑ k = 1 n k 2 = 6 n ( n + 1 ) ( 2 n + 1 )
Log in to reply
can you please tell how this proves that?
Log in to reply
We have the generating function ∑ n = 1 ∞ n 2 x n = ( 1 − x ) 3 x ( x + 1 ) . Multiplying through with ∑ n = 0 ∞ x n = 1 − x 1 gives ∑ n = 1 ∞ ( ∑ k = 1 n k 2 ) x n = ( 1 − x ) 4 x ( x + 1 )
Relevant wiki: Generating Functions
If A ( x ) is the generating function of { a n } , then 1 − x A ( x ) is the generating function of the partial sums of a n . Now, A ( x ) = x + x 2 is the generating function of the sequence { 0 , 1 , 1 , 0 , . . . , 0 , . . . } . Denote by { S a n i } the partial sums of the sequence { S a n i − 1 } , and define { S a n 0 } = { a n } . We have: S a n 1 = { 0 , 1 , 2 , 2 , . . . , 2 , . . . } and: S a n 2 = { 0 , 1 , 3 , 5 , 7 , . . . , 2 n − 1 , . . . } and: S a n 3 = { 0 , 1 , 4 , 9 , . . . , n 2 , . . . } and finally: S a n 4 = { 0 , 1 , 5 , 1 4 , 3 0 , . . . , 6 n ( n + 1 ) ( 2 n + 1 ) , . . . } . The 1975th element in this sequence is the answer.
Yes, exactly! (+1) That's the solution I had in mind! People who know about generating functions would probably be familiar with the generating function of n 2 , so, in my comment to Abhi's solution I took it from there. Then we take the generating function of the partial sums once more to find the answer.


