Triangle Problem
E is a point inside △ A B C such that A E = B E = B C and ∠ A B E = ∠ C B E = 2 0 ∘ . Find the measure of ∠ C A E .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
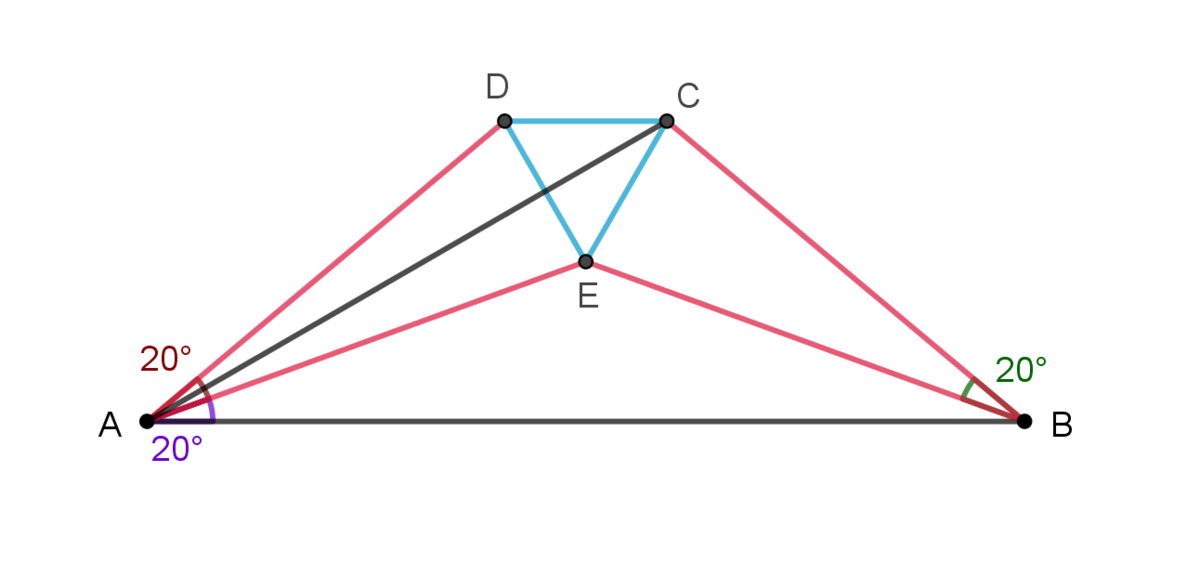 By doing extra construction as shown above we get an isosceles trapezoid
A
B
C
D
.
A
E
C
D
is a kite and its diagonals are perpendicular. Line segment
A
C
bisects
∠
D
A
E
therefore
∠
C
A
E
=
1
0
∘
By doing extra construction as shown above we get an isosceles trapezoid
A
B
C
D
.
A
E
C
D
is a kite and its diagonals are perpendicular. Line segment
A
C
bisects
∠
D
A
E
therefore
∠
C
A
E
=
1
0
∘
Hello! Would you mind explaining to me how you know that C E and C D have the same length?
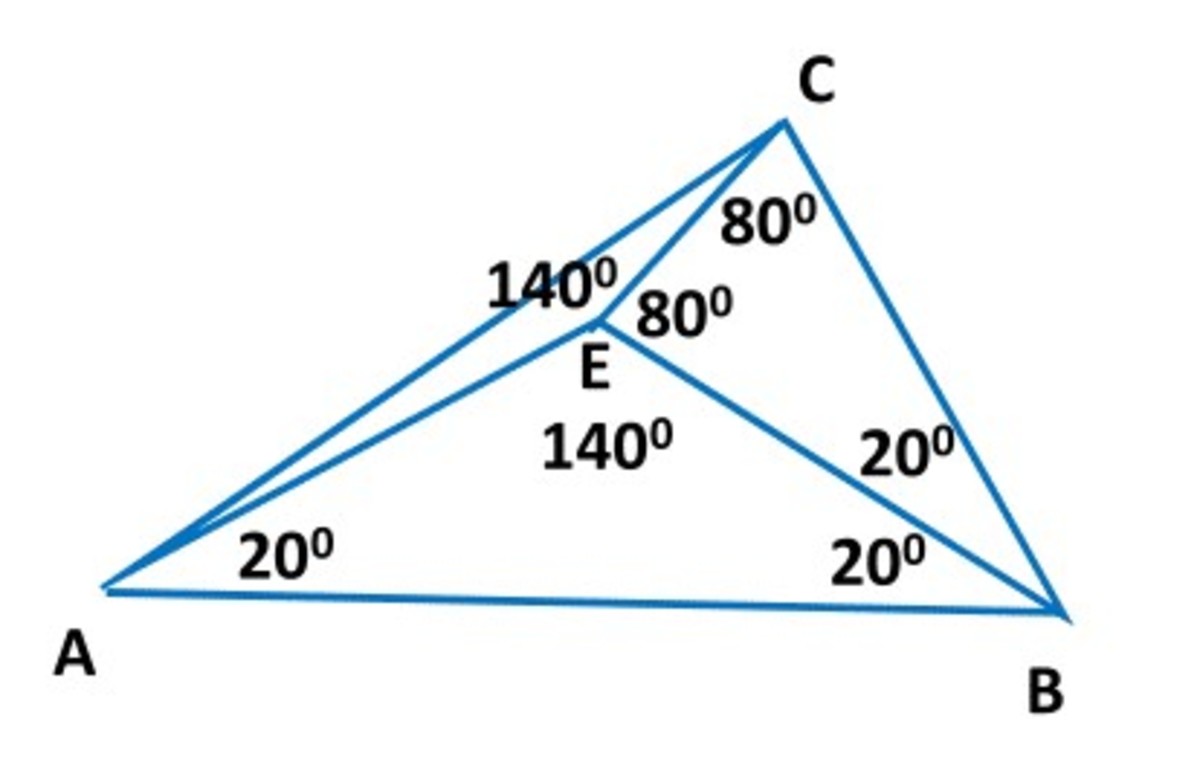 Some angle chasing gives the angles listed.
Some angle chasing gives the angles listed.
We can set A E = E B = B C = 1 .
E C = 2 × s i n ( 1 0 ∘ ) = 0 . 3 4 7 3
From the law of cosines in △ A C E we get A C = 1 . 2 8 5 6
From the law of sines ∠ C A E = a r c s i n ( A C C E ⋅ s i n ( 1 4 0 ∘ ) ) = 1 0 ∘
@Marta Reece Is there any way to solve this without using a Calculator????
Log in to reply
Probably, but I sure don't know it.
Let ∠ C A E = θ . Then ∠ A C E = 4 0 ∘ − θ . We have E C = 2 sin ( 1 0 ∘ ) and A E = 1 .
We shall repeatedly use the product to sum and sum to product formulas. https://brilliant.org/wiki/fundamental-trigonometric-identities-problem/#product-to-sum-formulas
Applying the law of sines in △ A C E , we obtain
\[ \begin{align}
\frac{\sin(\angle CAE)}{EC} &= \frac{\sin( \angle ACE)}{AE} \\ \frac{\sin(\theta)}{2\sin(10^\circ)} &= \sin(40^\circ - \theta) \\ \sin(\theta) &= 2\sin(10^\circ)\sin(40^\circ - \theta) \\ \sin(\theta) &= 2\sin(10^\circ)\cos(\theta + 50^\circ) & \text{as } \cos(\phi) = \sin(90^\circ - \phi) \\ \sin(\theta) &= \sin(\theta + 60^\circ) + \sin(-\theta - 40^\circ) \\ \sin(\theta) - \sin(\theta + 60^\circ) &= - \sin(\theta + 40^\circ) \\ \sin(\theta - 60^\circ) &= - \sin(\theta + 40^\circ) & \text{since } \sin(\theta - 60^\circ) + \sin(\theta + 60^\circ) = 2\sin(\theta)\cos(60^\circ) = \sin(\theta) \\ \sin(\theta - 60^\circ) + \sin(\theta + 40^\circ) &= 0 \\ 2\sin(\theta - 10^\circ)\sin(-50^\circ) &= 0 \\ \sin(\theta - 10^\circ) &= 0
\end{align} \]
Along with the fact that 0 ≤ θ ≤ 1 8 0 ∘ , we deduce that θ = 1 0 ∘ .
Define the 3 equal lengths each as S, AC = h, EC = f. Clearly, <BEA = 140, < BEC = 80, <AEC = 140. In triangle BEC, by Law of Cosines, F^2 = s^2 + s^2 - 2s^2 cos(20), f = .347296355S. In triangle AEC, by Law of Cosines, h^2 = f^2 + s^2 -2fs cos(140), h = 1.28557515S. In triangle AEC, by the Law of Sines, f/sin(x) = h/sin(140), x = 10. Ed Gray
 Since
A
E
=
B
E
, then
△
A
E
B
is an isosceles triangle. Draw
∠
C
B
D
, where
∠
C
B
D
=
2
0
°
clockwise. Extend
A
C
to
F
, where
F
is the intersection of
A
C
and
B
D
. Since
A
C
⊥
B
D
, then
△
A
F
B
is a right triangle. Note that
∠
A
B
F
=
3
∠
A
B
E
, then
△
A
F
B
is a 30-60 right triangle. Therefore,
∠
B
A
F
=
∠
B
A
E
+
∠
C
A
E
=
3
0
°
⟹
∠
C
A
E
=
1
0
°
.
Since
A
E
=
B
E
, then
△
A
E
B
is an isosceles triangle. Draw
∠
C
B
D
, where
∠
C
B
D
=
2
0
°
clockwise. Extend
A
C
to
F
, where
F
is the intersection of
A
C
and
B
D
. Since
A
C
⊥
B
D
, then
△
A
F
B
is a right triangle. Note that
∠
A
B
F
=
3
∠
A
B
E
, then
△
A
F
B
is a 30-60 right triangle. Therefore,
∠
B
A
F
=
∠
B
A
E
+
∠
C
A
E
=
3
0
°
⟹
∠
C
A
E
=
1
0
°
.
Hello! Would you mind explaining to me how you know that A C ⊥ B D ? (Also, what is D ?)