Hardcore solve for $x$ problem

$\begin{aligned} \sin^{-1} (m) & = \tan^{-1} (x^k) \\ \implies \tan^{-1} \left(\frac {m}{\sqrt{1-m^2}} \right) & = \tan^{-1} (x^k) \\ \frac {m}{\sqrt{1-m^2}} & = x^k & \small \blue{\text{Squaring both sides }} \\ \frac {m^2}{1-m^2} & = x^{2k} \\ m^2 & = (1-m^2)x^{2k} \\ \implies m^2 & = \boxed{\frac {x^{2k}}{1+x^{2k}}} \end{aligned}$

Since $\arctan \left( x \right) = \arcsin \left( {\frac{x}{{\sqrt {{x^2} + 1} }}} \right)$ we can just plug the argument into the formula and get the answer $\begin{array}{l} \arcsin \left( m \right) = \arcsin \left( {\frac{{{x^k}}}{{\sqrt {{x^{2k}} + 1} }}} \right)\\ {m^2} = \frac{{{x^{2k}}}}{{{x^{2k}} + 1}} \end{array}$ .

Let $\alpha = \arctan (x^k) = \arcsin (m)$ . Both $\arctan$ and $\arcsin$ return values between $\frac{\text{-}\pi}{2}$ and $\frac{\pi}{2}$ , so $\alpha$ will be an angle in quadrant I or quadrant IV. In either case, and using the fact that $\tan \alpha = x^k$ , we can draw $\alpha$ as shown below:

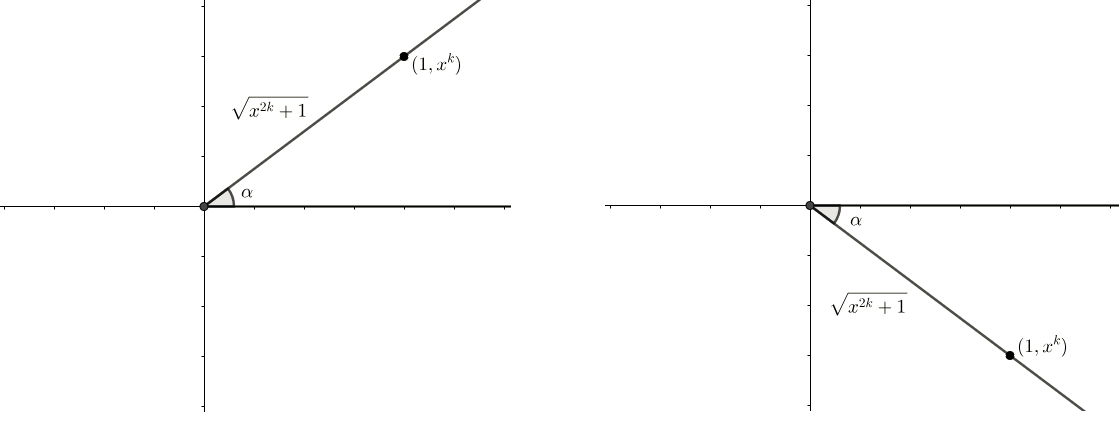
But we also have $\sin \alpha = m$ . Then

$\begin{array}{rcl} \sin \alpha &= \ \ m &= \ \ \dfrac{x^k}{\sqrt{x^{2k} + 1}} \\ \\ &\implies m^2 &= \ \ \boxed{\dfrac{x^{2k}}{x^{2k} + 1}} \end{array}$