Pizza Meetup

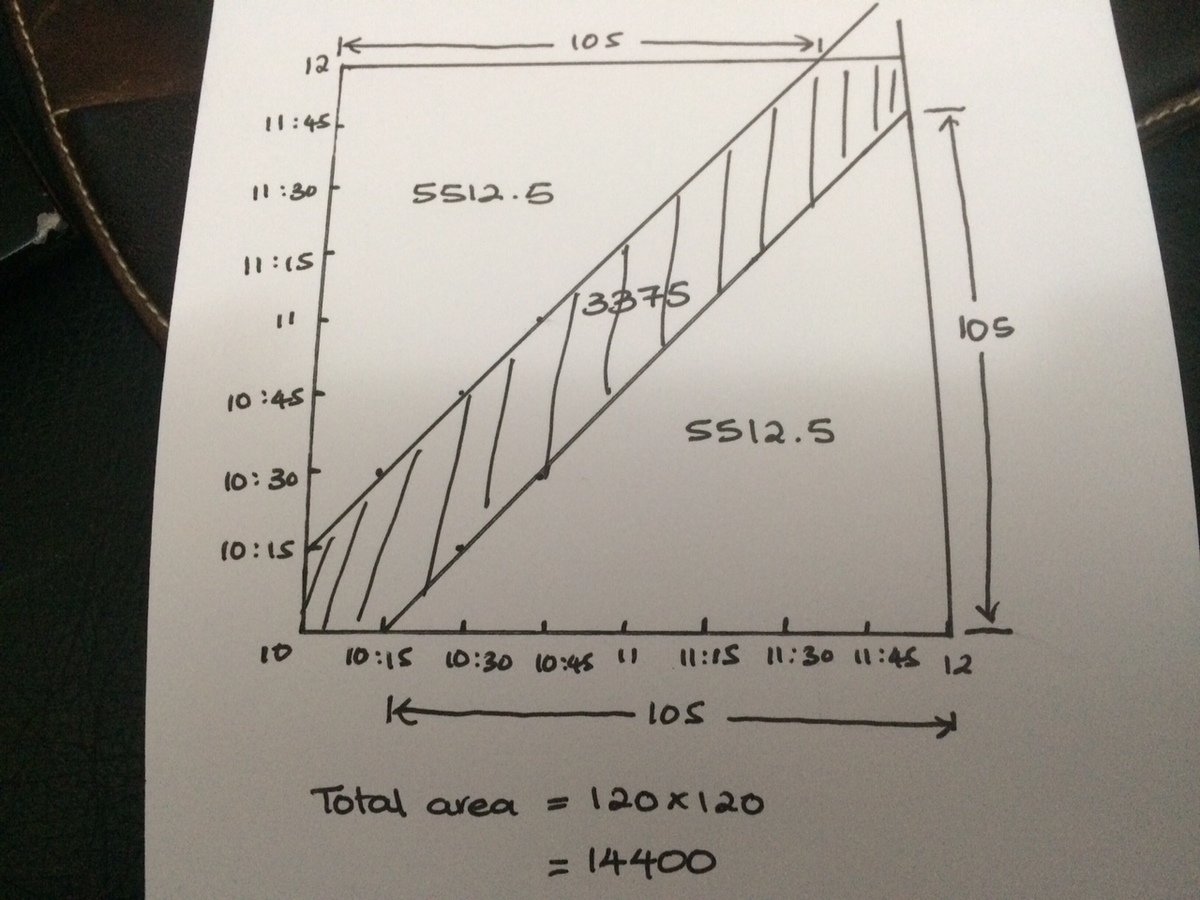I basically drew a graph to represent the possible times in which they could meet. E.g., If Dave arrives at 10:00 pm, Kathy must arrive no later than 10:15pm. If Dave arrives at 10:01 pm, Kathy must arrive no later than 10:16pm, and so forth. The 15 minutes leeway is shown on the graph which represents the opportunity of meeting, and the area representing that is equivalent to 3375 minutes. The total time available (possibility frontier)for which they could meet is 14,400 minutes. Hence, the probability that both Dave and Kathy were together at Pizza Place is 3375/14400=15/64

Without loss of generality, assume that Dave is the person that arrives first. Also, we realize that 15 minutes is 1/8 of the time between 10 pm and midnight (2 hours). There are 2 possiblities.

Case 1: Dave arrives between 10:00 pm and 11:45 pm. This is 7/8 of the total time. Then there is a 15 minute interval after this for Kathy to arrive. This is 1/8 of the total time. Therefore, the probability that Dave arrives between 10:00 pm and 11:45 pm and that he sees Kathy is 7/8*1/8=7/64

Case 2: Dave arrives between 11:45 pm and midnight. Then, because Kathy hasn't arrived yet (Dave was first to arrive by assumption), Kathy must arrive after Dave but before midnight, so Dave will see Kathy for certain. The probability of Dave arriving between 11:45 pm and midnight is 1/8, or 8/64.

The probability of the two meeting at all is simply the sum of these two cases. 7/64+8/64=15/64. 15 and 64 are relatively prime, and 15+64=79. So 79 is our final answer.

The problem can be considered as two events: Dave picking a time and then Kathy picking a time. Assuming random implies a uniform distribution:

for 75% of Dave's sample space (10:15 - 11:45) Kathy has a 30 minute interval to pick from (centered at Dave's time) to meet up with Dave. Otherwise stated, 75% of the time, there is a 25% probability of meeting each other.

the remaining 25% of the time, we first consider the interval between 10:00 - 10:15; the probability of them meeting up will depend on Dave's arrival time, given by the following function:

• p(x) = (x + 15)/120

where x represents the minutes past 10:00 that Dave arrives (as Kathy can arrive anywhere before that time or 15 minutes after).

We can calculate the expected value of the probability of them meeting up within this interval by integrating this function over the interval and dividing by the interval's size:

• $E(p(x)) = 1/15\int_{0}^{15} p(x) dx$

which evaluates to 3/16. Thus the expected probability that the will meet up in the interval of 10:00-10:15 is 18.75%. By symmetry this value also applies to the interval of 11:45-12:00.

Thus the composite probability that they will meet up between 10:00-12:00 is:

• 0.75(0.25) + 0.25(0.1875) = 15/64

• Let $t_d,\:t_k$ be the times that Dave and Kathy arrive at Pizza Palace, respectively. We need to assume their arrival times were independent from each other and uniformly distributed (see remark at the end). Let's get rid of all units by normalising: $\begin{aligned} d&:=\frac{t_d - \SI{10}{\hour}}{\SI{2}{\hour}}, &&&k&:=\frac{t_k - \SI{10}{\hour}}{\SI{2}{\hour}}&&&\Rightarrow&&&&(d,\:k)&\in[0;\:1]^2 \end{aligned}$

• Dave and Kathy meet if (and only if) they arrive within 15 minutes of each other: $\begin{aligned} |t_d-t_k|&\overset{!}{<}\SI{15}{\minute}&&&\Leftrightarrow&&&&|d-k|&=\frac{|t_d-t_k|}{\SI{2}{\hour}}\overset{!}{<}\frac{\SI{15}{\minute}}{\SI{2}{\hour}}=\frac{1}{8}\\ &&&& \Leftrightarrow&&&&d-\frac{1}{8}&<k<d+\frac{1}{8}&&&(*) \end{aligned}$

  We need to find the symmetric area bounded by the unit square $[0;\:1]^2$ and the two lines (*). A small sketch just like Randy's shows it's easier to subtract the two equal triangles from the unit square: $P(\text{Dave and Kathy meet}) = 1 - 2\times\frac{1}{2}\cdot\left(\frac{7}{8}\right)^2=\boxed{\frac{15}{64}}$

Rem.: The text implies independent arrival times ("both arrive [..] at two random times"), but there is no information how the arrival times are distributed. If we cannot assume a uniform distribution, we could not calculate the probability simply by measuring the area!