This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
First, compare the series with the infinite geometric series,
2 1 + 4 1 + 8 1 + 1 6 1 + ⋯ = 1 1 ∗ 2 1 + 2 ∗ 4 1 + 3 ∗ 8 1 + 4 ∗ 1 6 1 + ⋯
Clearly, every term in the bottom series is equal to or less than its term in the top series. Therefore, the sum we are looking for is less than 1.
Then, note that e 1 is less than 2 1 since 2 < e . Since the first term in the series is 2 1 and all the other terms are positive, the series converges to something greater than e 1 . The only option left among the possible answer choices is ln ( 2 ) so this must be the answer.
Gotta love multiple choice questions! I did it the same way.
Even I did it in this way...
i did that same way. But that's not the correct way. That's logic and not learning.
If you do it this way, why not just calculate the sum of the fist four and then compare?
I did it a very similar way as I have very little knowledge in what seems to be Maclaurin Series. But after looking at the real solution I feel the dumb.
Let ∣ x ∣ < 1 and y = ∑ n = 1 ∞ n x n
⟹ d x d y = ∑ n = 1 ∞ x n − 1 = 1 − x 1 ⟹ y = ∫ 0 x 1 − x 1 d x = ln ∣ 1 − x 1 ∣ .
Using x = 2 1 ⟹ ∑ n = 1 ∞ n 2 n 1 = ln ( 2 ) .
Oh, this was my approach too, but I didn't workout the exact formula. Just guessed the possible functions and selected the most appropriate answer
Log in to reply
Below is one of my posted problems which is an extension of the above problem :
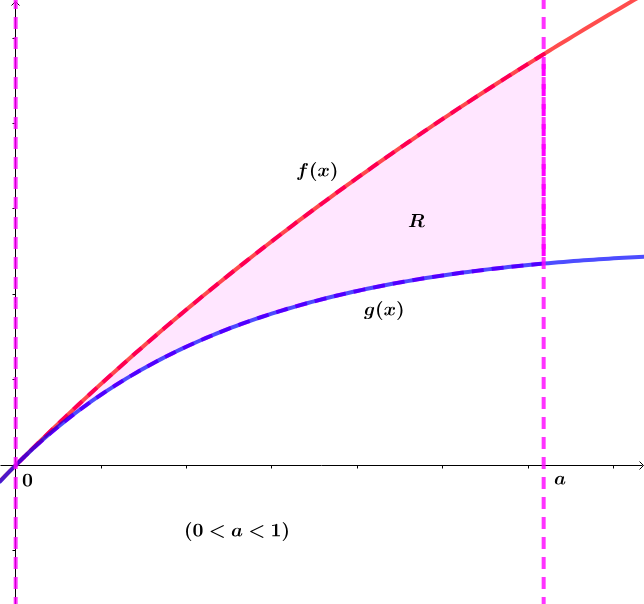
Let ∣ x ∣ < 1 and ( 0 < a < 1 ) .
If f ( x ) = ∑ n = 1 ∞ ( − 1 ) n + 1 n x n and g ( x ) = ∑ n = 1 ∞ ( − 1 ) n + 1 n x n and the region R bounded by f and g on [ 0 , a ] has area A R = a ln ( a + 1 ) − ( 2 a − 1 ) , find the real value of a and express the answer as the value of A R to six decimal places.
Share my solution:
Let f ( x ) = 2 x + 2 ⋅ 2 2 x 2 + 3 ⋅ 2 3 x 3 + ⋯ + k ⋅ 2 k x k + … , so question is asking f ( 1 ) .
Doing derivative, get
f ′ ( x ) = 2 1 + 2 2 x + 2 3 x 2 + 2 4 x 3 + … = 1 − x / 2 1 / 2 = 2 − x 1
Note that the function only converge when − 2 < x < 2 which didn't contradict our assumption.
So, take anti-derivative get
f ( x ) = ∫ f ′ ( x ) d x = ∫ 2 − x 1 d x = − ln ∣ 2 − x ∣ + C
Look back to the expression of f ( x ) , we know that f ( 0 ) = 0 , leads to C = ln 2 , so answer would be:
f ( 1 ) = − ln ∣ 2 − 1 ∣ + ln 2 = ln 2
Many great solutions were given, and this is a way to check your answer in Python:
sum([1/(n*2**n) for n in range(1, 100)])
we'll write f ( x ) = 1 x + 2 x 2 + ⋯ = ∑ n = 1 ∞ n x n
then, we will differentiate to get a geometric series f ′ ( x ) = 1 + x + x 2 + ⋯ = ∑ n = 1 ∞ x n = 1 − x 1
now we can integrate to get our equation back f ′ ( x ) = 1 + x + x 2 + ⋯ = ∑ n = 1 ∞ x n = 1 − x 1 u = 1 − x d u = − d x f ( x ) = − ∫ u 1 d u = − ln u = − ln ( 1 − x ) = ln 1 − x 1
we need to calculate f ( 2 1 ) , which is ln 1 − 2 1 1 = ln 2 − 1 2 = ln 2
As we have to add (1÷2) in the converging infinite series the answer is between 1 and 0.5 so the answer is ln2
This can be done through process of elimination.
( 2 ) 3 − 1 1 = n = 1 ∑ ∞ ( 2 ) n 2 n 1 < n = 1 ∑ ∞ n 2 n 1 < n = 1 ∑ ∞ 2 n 1 = 1
Since ( 2 ) 3 − 1 1 ≈ 0 . 5 4 7 and e 1 ≈ 0 . 3 6 8
the answer must be ln 2
More simple what @Jake Zweifler did.
Relevant wiki: Maclaurin Series
Considering the Maclaurin series of
ln ( 1 + x ) ln ( 1 − x ) ⟹ n = 1 ∑ ∞ n x n n = 1 ∑ ∞ n 2 n 1 = x − 2 x 2 + 3 x 3 − 4 x 4 + ⋯ = − n = 1 ∑ ∞ n x n = − ln ( 1 − x ) = ln ( 1 − x 1 ) = ln ( 1 − 2 1 1 ) = ln 2 for − 1 < x ≤ 1 Putting x = 2 1