Harmonic Mean and Infinite Sum

Algebra Level 4

∑ k = 1 ∞ 1 3 k a k \large \sum_{k=1}^\infty \frac{1}{3^ka_k}

A sequence { a n } \{a_n\} of real numbers is defined by a 1 = 20 , a 2 = 14 a_1=20,a_2=14 and for n ≥ 3 n\geq 3 , a n a_n is the harmonic mean of a n − 1 a_{n-1} and a n − 2 a_{n-2} .

If the infinite sum above can be represented in the form of p q \frac pq for some relatively prime positive integers p p and q q , find p + q p+q .


The answer is 403.

View wiki
Russelle Guadalupe by Russelle Guadalupe , 25, Philippines

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Patrick Corn
May 27, 2015

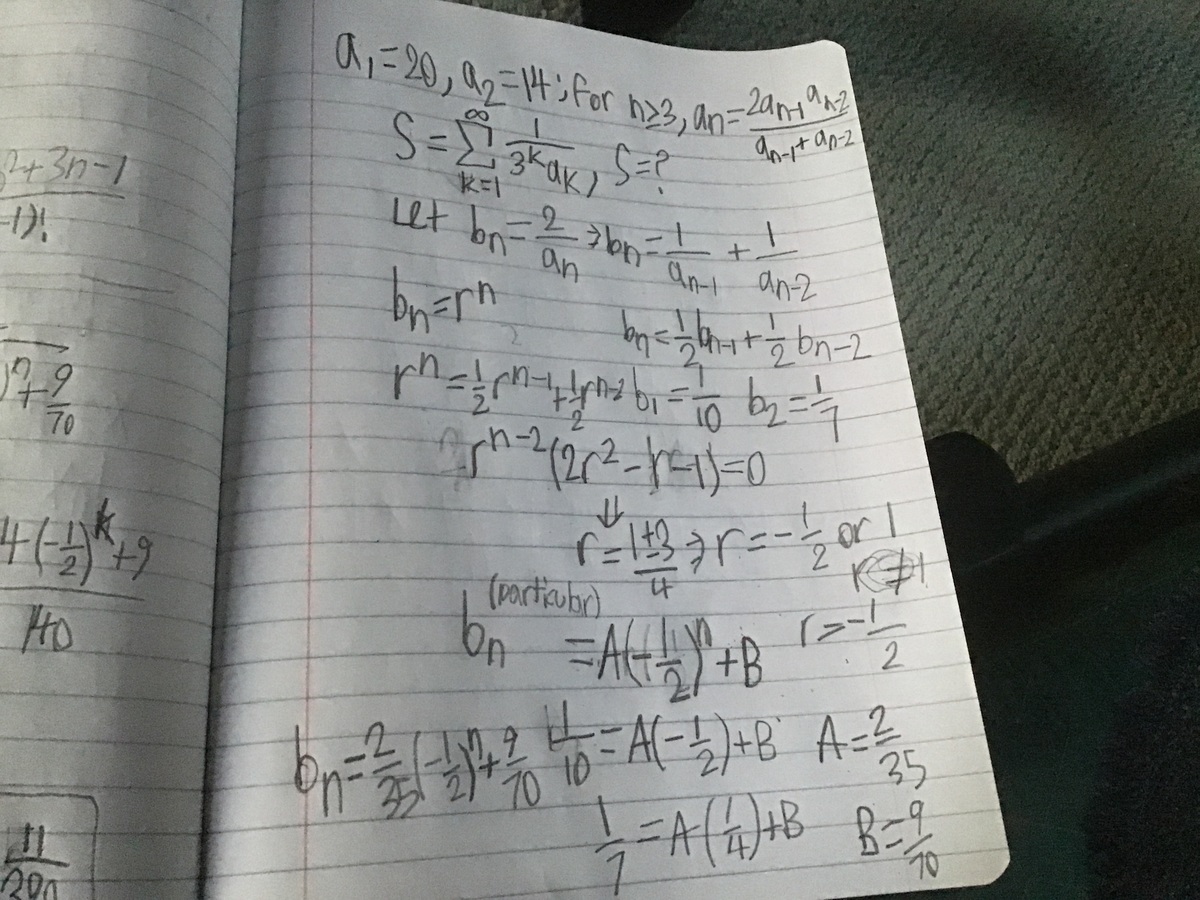
Let S S be the sum. Then S = 1 3 a 1 + 1 9 a 2 + 1 2 ∑ k = 3 ∞ ( 1 3 k a k − 1 + 1 3 k a k − 2 ) = 1 3 a 1 + 1 9 a 2 + 1 6 ∑ b = 2 ∞ 1 3 b a b + 1 18 ∑ c = 1 ∞ 1 3 c a c \begin{aligned} S &= \frac1{3a_1} + \frac1{9a_2} + \frac12 \sum_{k=3}^{\infty} \left( \frac1{3^k a_{k-1}} + \frac1{3^k a_{k-2}} \right) \\ &= \frac1{3a_1} + \frac1{9a_2} + \frac16 \sum_{b=2}^{\infty} \frac1{3^b a_b} + \frac1{18} \sum_{c=1}^{\infty} \frac1{3^c a_c} \end{aligned} where b = k − 1 b = k-1 and c = k − 2 c = k-2 .

So S = 1 3 a 1 + 1 9 a 2 + 1 6 ( S − 1 3 a 1 ) + 1 18 S S = \frac1{3a_1} + \frac1{9a_2} + \frac16 \left( S - \frac1{3a_1} \right) + \frac1{18} S and solving for S S leads to S = 45 126 a 1 + 1 7 a 2 S = \frac{45}{126a_1} + \frac1{7a_2} .

Plugging in a 1 = 20 , a 2 = 14 a_1 = 20, a_2 = 14 gives S = 11 392 S = \frac{11}{392} , so the answer is 403 \fbox{403} .

6 Helpful 0 Interesting 0 Brilliant 1 Confused
Aareyan Manzoor
Jun 16, 2015

2 Helpful 0 Interesting 1 Brilliant 0 Confused

Do not mind the "r≠1" part.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...