Harmonic ( Motion + Inequality)
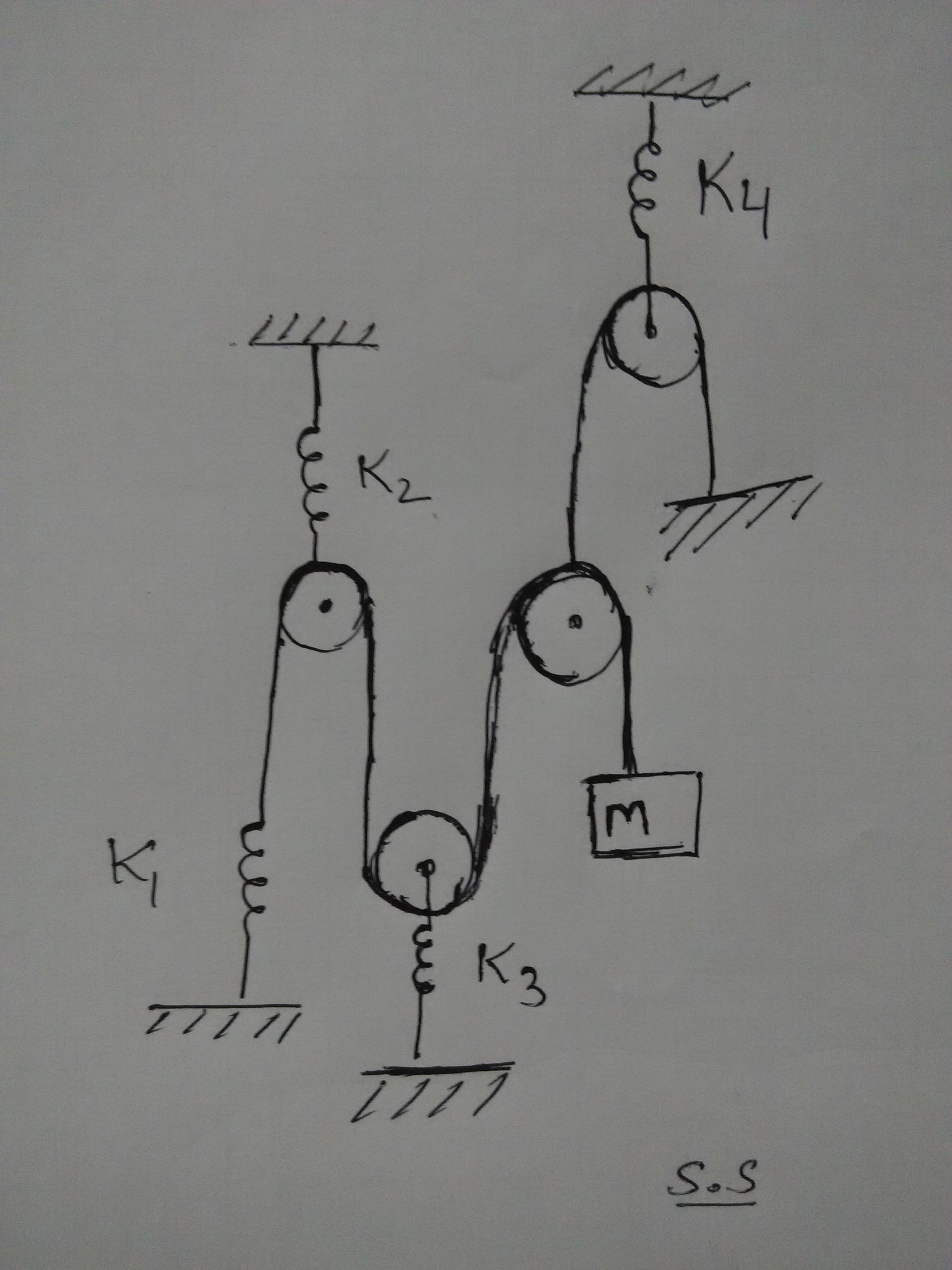 In the given arrangement there are four springs with constants
k
1
,
k
2
,
k
3
and
k
4
(as shown in the figure). The block of mass
m
=
1
kg is slightly displaced from its mean position. Find the minimum possible value of the period of the simple harmonic motion of this system.
In the given arrangement there are four springs with constants
k
1
,
k
2
,
k
3
and
k
4
(as shown in the figure). The block of mass
m
=
1
kg is slightly displaced from its mean position. Find the minimum possible value of the period of the simple harmonic motion of this system.
Assumptions and Details
- k 1 + k 2 + k 3 + k 4 = 4 π 2
- Assume all pulleys are ideal.
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Good problem! I noticed some problems in the diagram and in the text, but none of them affect the understanding of the question.
Let x 1 , x 2 , x 3 , x 4 be the spring displacements away from the attachment point Let y be the downwards displacement of the mass m.
By the configuration of the pulleys, we can write the relation between the mass displacement and the displacements of the springs:
y = 1 × x 1 + 2 × x 2 + 2 × x 3 + 4 × x 4
To shorten the notation, we create coefficients c i such that y = ∑ j = 1 4 c j x j , i.e., c 1 = 1 , c 2 = c 3 = 2 , c 4 = 4 .
To obtain the equations of motion we will calculate the lagrangian of the system given by L = T − V where T is the knectic energy and V is the potential energy of the system:
V = j = 1 ∑ 4 2 k j x j 2 − m g y
T = 2 m y ˙ 2
L = T − V = 2 m y ˙ 2 − j = 1 ∑ 4 2 k j x j 2 + m g y = 2 m ( j = 1 ∑ 4 c j x ˙ j ) 2 − j = 1 ∑ 4 2 k j x j 2 + m g ( j = 1 ∑ 4 c j x j )
Now we can use the Euler-Lagrange equation to obtain the equations of motion for each of the 4 coordinates:
d t d ( ∂ x i ˙ ∂ L ) = ∂ x i ∂ L
∂ x i ˙ ∂ L = m c i ( j = 1 ∑ 4 c j x ˙ j ) ⇒ d t d ( ∂ x i ˙ ∂ L ) = m c i ( j = 1 ∑ 4 c j x ¨ j )
∂ x i ∂ L = m g ∂ x i ∂ ( j = 1 ∑ 4 c j x j ) − k i x i ⇒ ∂ x i ∂ L = m g c i − k i x i
Then the equations of motion are:
m c i ( j = 1 ∑ 4 c j x ¨ j ) = m g c i − k i x i for i = 1 , … , 4
Let us rewrite the equations to separate the nonhomogeneous term:
j = 1 ∑ 4 c j x ¨ j + ( m c i k i ) x i = g for i = 1 , … , 4
The minimum possible value of the period is always the period of the fastest normal mode. To get it, we can calculate the frequencies of the normal mode which can be done by assuming that all springs oscilate in the same base frequency α :
x i = A i e i α t ⇒ x ¨ i = − α 2 A i e i α t
Substituting these values into the equations of motion and discarding the nonhomogeneous term, we obtain:
α 2 j = 1 ∑ 4 c j A j − ( m c i k i ) A i = 0 for i = 1 , … , 4
These equations can be written in matrix form as follows:
M A = 0 where M i j = α 2 c j + δ i j m c i k i
To obtain a non-trivial solution for the system, we must have det ( M ) = 0 which results in:
α = ± ∑ j = 1 4 k i c i 2 1
This alpha value corresponds to the only normal mode of the system and has the following period:
T = ∣ α ∣ 2 π = 2 π j = 1 ∑ 4 k i c i 2
To obtain the minimum possible value with the restriction that ∑ j = 1 4 k i = 4 π 2 we can use the Jensen's inequality.
The Jensen's inequality for a convex function φ for weigths a i and points z i is:
φ ( ∑ a i ∑ a i z i ) ≤ ∑ a i ∑ a i φ ( z i )
For φ ( x ) = x 1 , a i = c i , and z i = c i k i we obtain:
∑ j = 1 4 c j c j k j ∑ j = 1 4 c j ≤ ∑ j = 1 4 c j ∑ j = 1 4 c j k j c j ⇒ ∑ j = 1 4 k j 1 + 2 + 2 + 4 ≤ 1 + 2 + 2 + 4 ∑ j = 1 4 k j c j 2 ⇒ 8 1 ≤ 4 π 2 j = 1 ∑ 4 k j c j 2 ⇒ 9 ≤ 2 π j = 1 ∑ 4 k j c j 2 ⇒ T ≥ 9
So the minimum possible value of the period of the simple harmonic motion of this system is 9 seconds.
Writing constraints we arrive at the relation x(1)+2x(2)+2x(3)+4x(4)=x where each of x(i) represent either elongation or compression in ith spring. Also as pulleys are ideal(massless) using NLM we can obtain relation between each of x(i) and x1 (convince yourself why I am am interested in relation between these two variables explicitly) and after all these manipulations use AM-HM inequality to arrive at the answer