Harmonic number approximation

$\large \displaystyle \gamma = \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac1k - \ln(n)$

Where $\gamma$ is the Euler–Mascheroni constant

Since $10^{12}$ is large:

$\large \displaystyle \gamma \approx \sum_{k=1}^{10^{12}} \frac1k - \ln(10^{12})$

$\large \displaystyle \sum_{k=1}^{10^{12}} \frac1k \approx \gamma + 12\ln(10) = 28.21...$

$\color{#3D99F6} \boxed{\large \displaystyle \left \lfloor \sum_{k=1}^{10^{12}} \frac1k \right \rfloor = 28 }$

Let's represent the sum $\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{10^{12}}$ as the total area of a set of rectangles in the xy-plane.

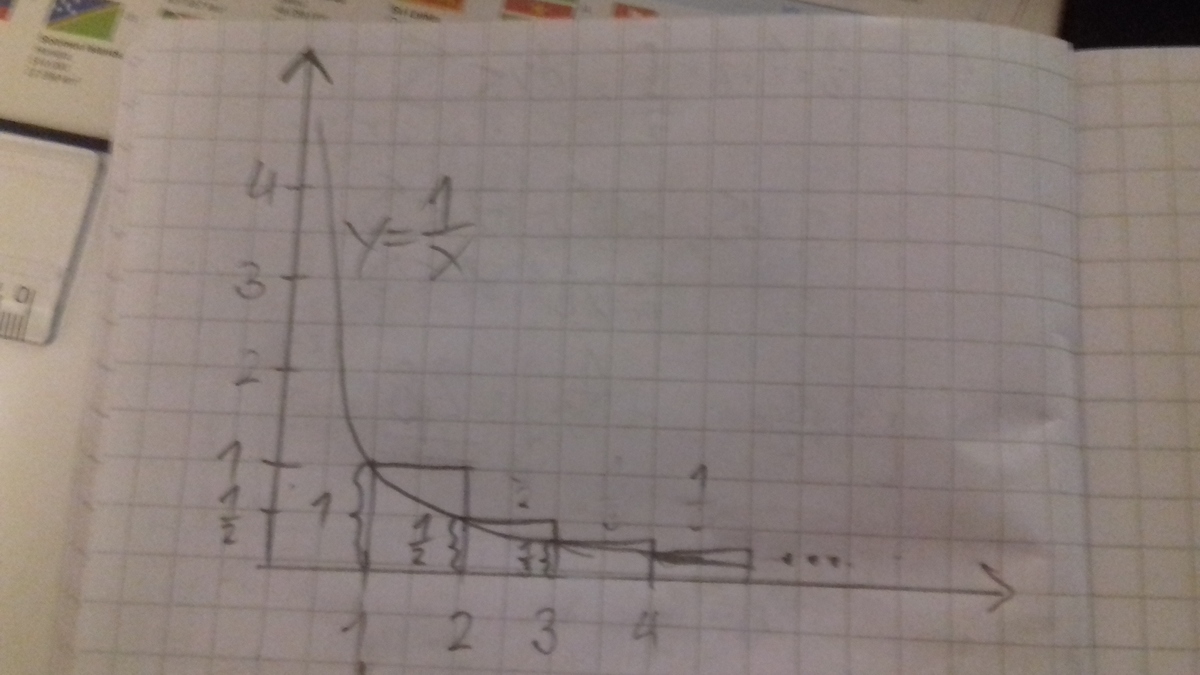
As it can be seen in the picture, the hyperbola $y=\frac{1}{x}$ goes through the upper left corners of the rectangles and goes below the tops of the rectangles. This means, the area between $x=1$ , $x=10^{12}+1$ , $y=\frac{1}{x}$ and the x-axis is smaller than the total area of the rectangles. We get

$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{10^{12}} > \int_1^{10^{12}+1}(\frac{1}{x}dx)>\int_1^{10^{12}}(\frac{1}{x}dx)$

$\int_1^{10^{12}}(\frac{1}{x}dx)=\ln(10^{12})-\ln(1)=12\ln(10) \approx 27,63>27$

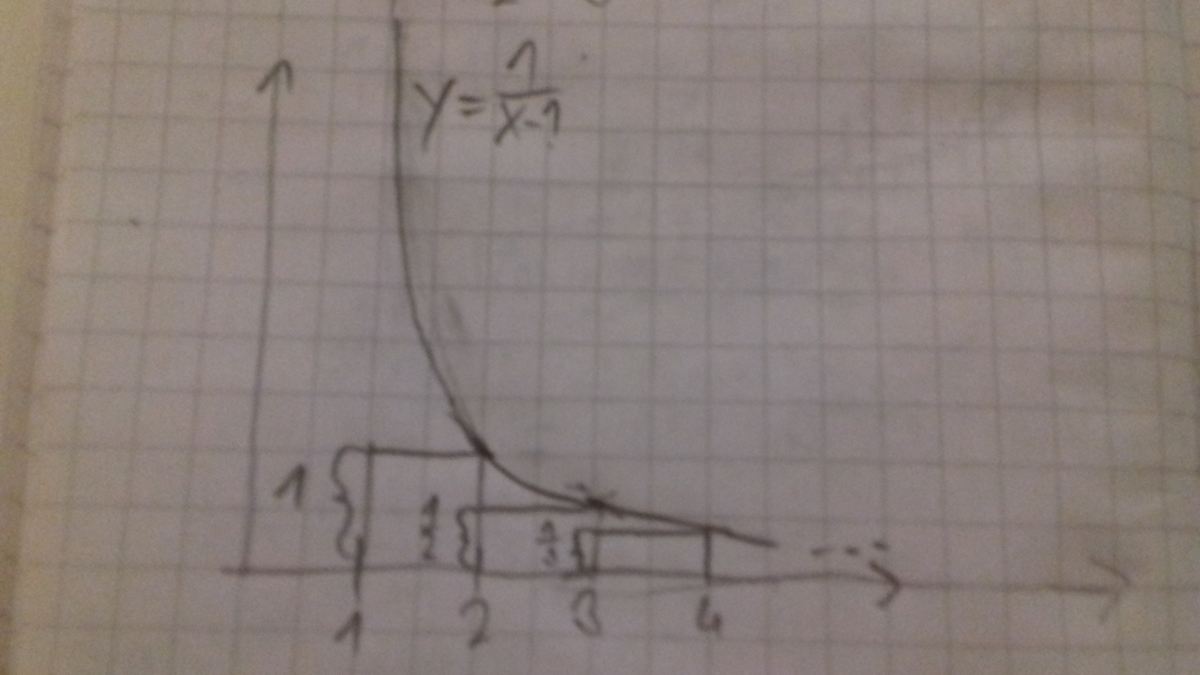
as seen in the second picture, the hyperbola $y=\frac{1}{x-1}$ goes through the upper right corners of the rectangles and otherwise above them. This means, the total area of the first rectangle and the area between $x=2$ , $x=10^{12}+1$ , $y=\frac{1}{x-1}$ and the x-axis is greater than the total area of all rectangles. We get

$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{10^{12}} < 1+ \int_2^{10^{12}+1}(\frac{1}{x-1}dx)$

$1+ \int_2^{10^{12}+1}(\frac{1}{x-1}dx)=1+\ln(10^{12})-\ln(1) = 1+\ln(10^{12}) \approx 28,631<29$

Now we know that $27<\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{10^{12}}<29$ , thus the floor function of the sum is either equal to 28 or 29. Let's prove it's 28 by showing that $28<\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{10^{12}}$ :

By the argument used above, we get

$1+ \frac{1}{2}+ \frac{1}{3}+ \frac{1}{4} + \frac{1}{5}+ \frac{1}{6}+ \int_7^{10^{12}}(\frac{1}{x}dx )< 1+ \frac{1}{2}+ \frac{1}{3}+ \frac{1}{4} + \frac{1}{5}+ \frac{1}{6}+ \int_7^{10^{12}+1}(\frac{1}{x}dx) < \frac{1}{1}+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{10^{12}}$

$1+ \frac{1}{2}+ \frac{1}{3}+ \frac{1}{4} + \frac{1}{5}+ \frac{1}{6}+ \int_7^{10^{12}}(\frac{1}{x}dx) = 1+ \frac{1}{2}+ \frac{1}{3}+ \frac{1}{4} + \frac{1}{5}+ \frac{1}{6} + 12 \ln(10) - \ln (7) \approx 28,135 > 28$

We get $28<\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{10^{12}}<29$ which proves that $\lfloor \frac{1}{1}+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{10^{12}} \rfloor = \boxed{28}$