Harmonic spring

Classical Mechanics Level 2

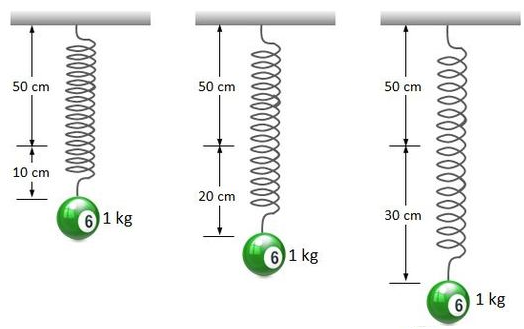
When a ball with mass 1 kg 1\text{ kg} is hung on a 50 cm 50\text{ cm} long spring, the length of the spring is increased by 10 cm 10\text{ cm} in steady state, as shown in the far left diagram. Now, suppose that we pull this ball further down and let it go. Then it will show simple harmonic oscillations. What will be the periods of these oscillations when we pull down the ball by 10 10 cm and 20 20 cm, respectively, as shown in the middle and right diagrams above?

Gravitational acceleration is 10 m/s 2 10 \text{ m/s}^2 .

0.2 π 0.2\pi seconds, 0.2 π 0.2\pi seconds 0.2 π 0.2\pi seconds, 0.4 π 0.4\pi seconds 0.1 π 0.1\pi seconds, 0.2 π 0.2\pi seconds 0.4 π 0.4\pi seconds, 0.2 π 0.2\pi seconds

View wiki
Lakshan Dumpa by Lakshan Dumpa , 24, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Vishal Sharma
Apr 11, 2014

Time period of Harmonic motion is independent of amplitude.. And is equal to 2 p i m k 2pi\sqrt{\frac{m}{k}}

23 Helpful 0 Interesting 1 Brilliant 0 Confused

life is always easy when basics are within us

Bhuvana Datta - 7 years ago

thanks for answer. can you explain why 2pi into root over l divided by g formula isn't use here ?

Sumon Shuvo - 5 years, 2 months ago

Log in to reply

thats the formula for a pendulum in small angle oscillations, not a spring

Rohan Joshi - 4 months, 1 week ago

its 2 pi (l/g)^0.5........in the second case it should have been 0.2pi*2^1/2

Sayam Chakravarty - 7 years ago

Hey, I went to level 2 of this particular question and I accidently selected the wrong option and lost it... Can I proceed to level 3 of this kind?? Please, tell me a way to find this type's level 3.... Please!!!

Rohit Imandi - 7 years, 1 month ago
Bernardo Sulzbach
Jun 24, 2014

It is NOT necessary to calculate k.

But I will write how to do the whole thing.

( 1 kg ) ( 10 m s − 2 ) = k ⋅ ( 0.1 m ) (1\text{ kg})(10 \text{ m s}^{-2})=k\cdot{}(0.1 \text{ m}) k = 100 N m − 1 k=100 \text{ N m}^{-1} T = 2 π m k = 2 π 1 kg 100 N m − 1 T=2\pi{}\sqrt{\frac{m}{k}}=2\pi{}\sqrt{\frac{1 \text{ kg}}{100 \text{ N m}^{-1}}} T = 0.2 π s T=0.2\pi{} \text{ s}

Note that, as T does not vary with amplitude (but only with mass and spring constant), T 1 = T 2 T_1=T_2

10 Helpful 0 Interesting 0 Brilliant 1 Confused
Alinjar Dan
Apr 22, 2014

so easy. T is independent of amplitude. That is = 2*3.148root of(m/k)

5 Helpful 0 Interesting 0 Brilliant 0 Confused

You are right. I solved this problem in this process.

Arghyanil Dey - 7 years, 1 month ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...