Harry Potter's Magical Geometry!
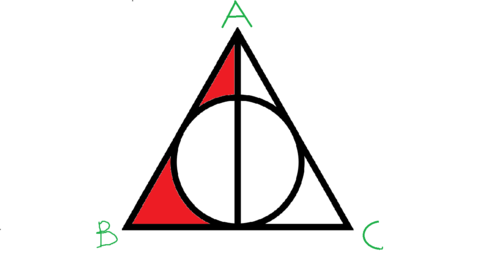 In the given figure ,
Δ
A
B
C
is an equilateral triangle with side as 1 unit.
In the given figure ,
Δ
A
B
C
is an equilateral triangle with side as 1 unit.
The given circle is the in-circle of Δ A B C
If Area of red colored region can be expressed as:
d a b − c where a , b , c , d ∈ N , b is independent of a perfect square ,
Find a + b + c + d
Details and Assumptions :-
- Take π as 7 2 2 .
The answer is 214.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Overrated! Good question though!
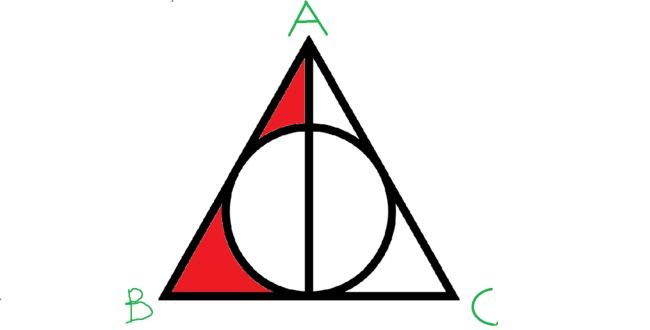
Area of △ A B C = 4 3
The we have that height since A also is a median and a bisector so radii of the circle will be 3 height = 3 2 3 = 6 3
Area of the circle is ( 6 3 ) 2 × 7 2 2 = 4 2 1 1
Now shaded area is 2 △ A B C − c i r c l e = 2 4 3 − 4 2 1 1 = 1 6 8 2 1 3 − 2 2
∴ a + b + c + d = 2 1 + 3 + 2 2 + 1 6 8 = 2 1 4
I n e q u v i l a t e r a l Δ , A r e a Δ = 4 3 , I n r a d i u s , r = 2 1 c i r c u m r a d i u s R ∴ r = 2 1 ∗ 4 ∗ A r e a a ∗ b ∗ c = 2 1 ∗ 4 ∗ 4 3 1 ∗ 1 ∗ 1 = 2 ∗ 3 1 ⟹ A r e a o f c i r c l e = 7 2 2 ∗ 1 2 1 = 7 ∗ 1 2 2 2 ∴ s h a d e d a r e a = 2 1 ∗ { 4 3 − 8 4 2 2 } = 1 6 8 2 1 3 − 2 2 . a + b + c + d = 2 1 + 3 + 2 2 + 1 6 8 = 2 1 4
How is this related to Harry Potter?
Since the circle is inscribed in an equilateral triangle, the altitude is the perpendicular bisector that goes through the center of the circle. Connect edge B to the center of the circle, call it O
Let the perpendicular bisector that starts at A intersect as D on B C
O D is the radius
B O is a perpendicular bisector that goes through the center of the circle. Thus, ∠ O B C = 3 0 , ∠ D O B = 6 0 and ∠ O D B = 9 0
Using the properties of 30-60-90 triangle, O D = 2 3 1
Area of this semicircle is 2 π ( 2 3 1 ) 2 which is 2 4 π
Area of an equilateral triangle is 4 3 a 2
Substitute a = 1 and divide by 2 , because it's half of the triangle, we get 8 3
Subtract the area of the half triangle and the semicircle: 8 3 − 2 4 π
Which simplifies to 1 6 8 2 1 3 − 2 2
Thus, our answer is a + b + c + d = 2 1 + 3 + 2 2 + 1 6 8 = 2 1 4
length of the median = (1/2)(square root of 3)
length of the radius = (length of the median)/3 = (1/6)(square root of 3)
area of the red region =
(1/2)(1/2) (1/2)(square root of 3) - (1/2)(22/7) [(1/6)(square root of 3)]^2 =
[(21)(square root of 3) - 22]/168
a = 21 , b = 3 , c = 22 and d = 168
Then
a + b + c + d = 214
Area of Δ A B C = 4 3 × 1 2 = 4 3
Semi-perimeter s = 2 1 + 1 + 1 = 2 3 , Let r be the inradius.
Area of Δ A B C = r . s ⇒ 4 3 = 2 3 r ⇒ r = 6 3
Area of in-circle = π r 2 = 7 2 2 × ( 6 3 ) 2 = 7 2 2 × 3 6 3 = 4 2 1 1
Area of shaded region = 2 Area of triangle ABC - Area of in-circle
Area of shaded region = 2 4 3 − 4 2 1 1 = 1 6 8 2 1 3 − 2 2
⇒ a + b + c + d = 2 1 + 3 + 2 2 + 1 6 8 = 2 1 4