Harvard MIT MT

Let A B C be a triangle with A B = 5 , A C = 4 , B C = 6 . The angle bisector of C intersects side A B at X . Points M and N are drawn on sides B C and A C , respectively, such that X M ∥ A C and X N ∥ B C . Compute the length M N .
The answer is 2.244.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
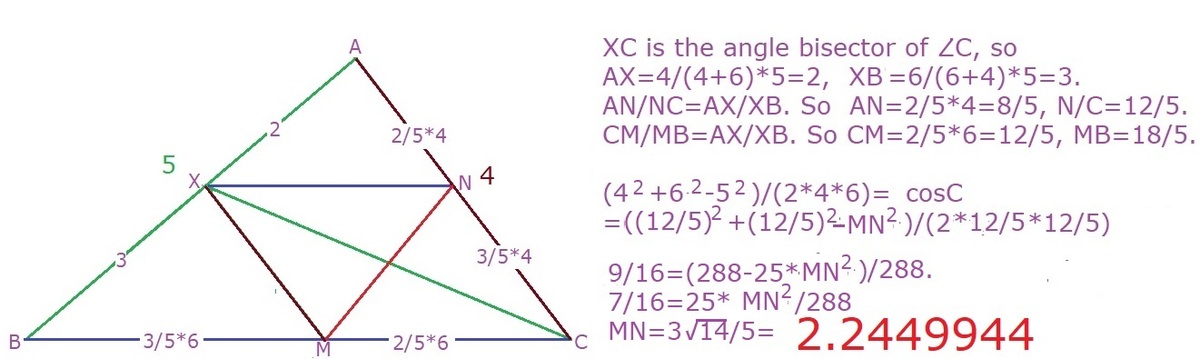
Good application of law of cosines.
Then MIT would have been as busy as an airport....
Log in to reply
Ya maybe but its environment is quite different than examples like an airport.
Harvard, MIT are you kidding me! >::

Missed because of calculation mistake, as normal with me!!
Log in to reply
Nice Solution sir!
Ya I know it feels too bad when we do mistake due to calculation mistake but I got this one.Doesnt seem to be of Harvard MIT.
It's easy to see that AXN and XBM are both similar to ABC. By the angle bisector theorem, we have AX = 2, XB = 3. Thus XN = XM = 12/5, using our similar triangles..
By parallel lines XN and BC, with transversal NM, we see that angles NMC and XNM are congruent. Additionally, by the smaller similar triangles which form straight angle AXB with angle NXM, we see that NXM is congruent to angle ACB. This means that XNM and CNM are similar.
Observe that XNMB is a parallelogram so that AX = BM = 18/5, which can be found using similar triangles. Now this means CM = 12/5, so we have that triangles XNM and CNM are in fact congruent.
A little formula for the length of angle bisector CX (or even Stewart's theorem) gives that CX = 3√2. Suppose CX and NM meet at D. Since CX is an angle bisector and CNM is isosceles, CD is an altitude. Additionally, XNCM is a parallelogram so that D is the midpoint of CX.
Now we have the hypotenuse and one leg of right triangle CDN, so DN can be calculated using the Pythagorean theorem, and furthermore doubled to get MN since D is also a midpoint.
I am sparing the calculations because I am on mobile, but it comes out to MN = 6/5 * √(7/2) ~ 2.24.
would you mind explain the angle bisector theorem further?
Log in to reply
The angle bisector theorem states that (using the points in this example) AX/AC = BX/BC. Then using AX + BX = AB, you can solve for AX and BX.
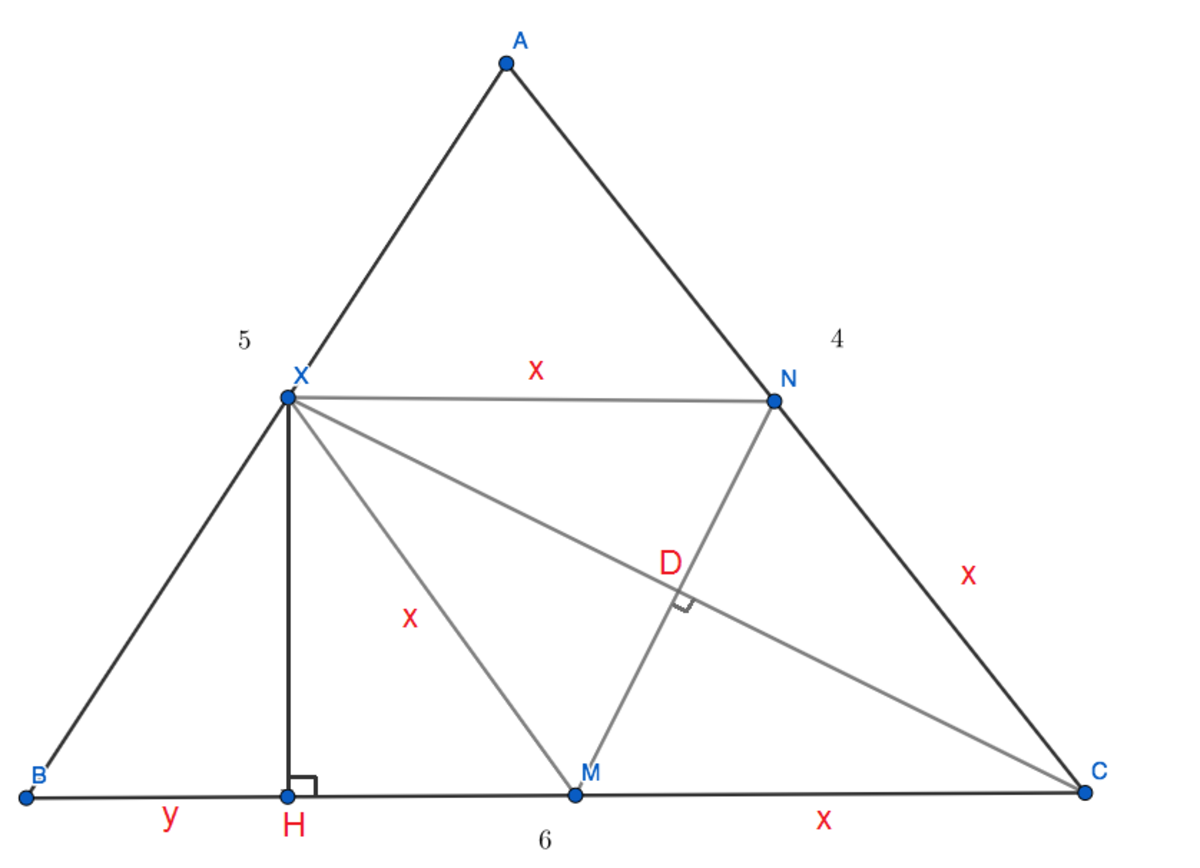
It is clear that X N C M is a parallelogram. X C is a diagonal of X N C M which bisects this parallelogram's angle ∠ M C N . A property of a rhombus is that its diagonals bisect their corresponding angles, which means that X N C M is not only a parallelogram, but a rhombus as well. So, X N = N C = M C = X M = x .
Because X M ∣ ∣ A C and X N ∣ ∣ B C , △ A B C is congruent to both △ X B M and △ A X N
We can find the length of x from the congruence between △ A B C and △ A X N :
B C X N = A C A N
X N = x
A N = A C − N C = 4 − x
6 x = 4 4 − x ⇒ x = 5 1 2
Using congruence between △ A B C and △ X B M :
A B X B = A C X M
X B = A C X M × A B = 4 x × 5 = 3
Now, we pick a point H on side B C such that X H ⊥ B C , and let y = B H . By Pythagoras, we have:
X B 2 − B H 2 = X M 2 − H M 2 = X C 2 − H C 2 = X H 2
Now, we find y like this:
H M = B C − M C − y = 6 − x − y
X B 2 − B H 2 = X M 2 − H M 2
9 − y 2 = x 2 − ( 6 − x − y ) 2
9 − y 2 = ( 5 1 2 ) 2 − ( 5 1 8 − y ) 2
Solving this equation, we get that y = 4 9 So, we can now determine the length of X C :
X C 2 = H C 2 + X B 2 − B H 2 = ( 6 − y ) 2 + 9 − y 2 = 1 8
Now, another property of a rhombus is that its diagonals are perpendicular to each other and bisect each other. Let D be the point of intersection of X N C M 's diagonals, X C and M N . Now we have:
D M 2 + D C 2 = ( 2 M N ) 2 + ( 2 X C ) 2 = 4 M N 2 + 4 X C 2 = M C 2 = x 2 .
Finally:
M C = 4 x 2 − X C 2 = 4 × ( 5 1 2 ) 2 − 1 8 = 5 3 1 4 ≈ 2 . 2 4 4
By the angle bisector theorem, A C A X = B C B X , or 4 A X = 6 5 − A X , which solves to A X = 2 , which means B X = 5 − 2 = 3 .
△ A X N ∼ △ A B C by AA similarity (since ∠ A is shared and ∠ C ≅ ∠ A N X by corresponding angles), so A X X N = A B B C , or 2 X N = 5 6 , which solves to X N = 5 1 2 .
Likewise, △ B X M ∼ △ A B C by AA similarity (since ∠ B is shared and ∠ A ≅ ∠ B X M by corresponding angles), so B X X M = A B A C , or 3 X M = 5 4 , which solves to X M = 5 1 2 .
Since ∠ C ≅ ∠ A N X by corresponding angles, and ∠ A N X ≅ ∠ N X M by alternate interior angles, ∠ C ≅ ∠ N X M .
By the law of cosines on △ A B C , cos C = 2 ⋅ 4 ⋅ 6 4 2 + 6 2 − 5 2 = 1 6 9 . And by the law of cosines on △ N X M , cos N X M = cos C = 2 ⋅ ( 5 1 2 ) ⋅ ( 5 1 2 ) ( 5 1 2 ) 2 + ( 5 1 2 ) 2 − x 2 . So 1 6 9 = 2 ⋅ ( 5 1 2 ) ⋅ ( 5 1 2 ) ( 5 1 2 ) 2 + ( 5 1 2 ) 2 − x 2 , which solves to x = 5 3 1 4 ≈ 2 . 2 4 4 .