Have a pure geometric solution?
In the triangle A B C , the altitude, angle bisector and the median from C divide ∠ C in four equal angles. Find the measure of the smallest angle of △ A B C in degrees.
The answer is 22.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Here we go:
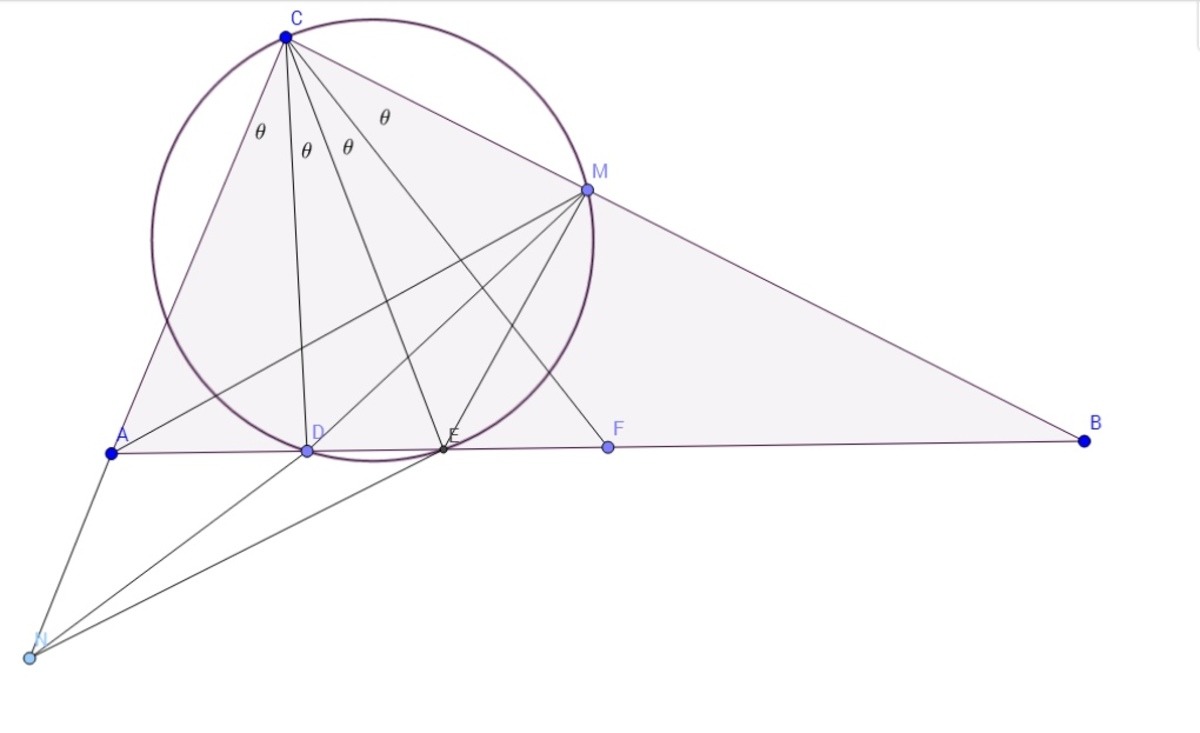
Let D , E , F respectively be foot of altitude, foot of angle bisector, foot of median - all from C to A B .
Drop a perpendicular from E to B C in the point M and let N be the intersection of M D , A C .
Then C D E M is cyclic. Hence,
∠ C M D = ∠ C E D = ∠ C A D .
It follows that triangle △ C M N ≈ △ C A B .
This implies that C D is the median from C in triangle C M N , hence A M E N is a parallelogram.
Finally, A N ∥ M E and since M E ⊥ B C , it follows that A C ⊥ B C .
Hence, smallest angle is ∠ B = 2 2 . 5 0 .
Suggestion : You should write one assumption: The angle has to be given in degrees. I almost fail his question due to this assumption.
Log in to reply
Thanks. I've updated the problem statement to reflect this. Those who previously answered 2 2 . 5 ÷ π 1 8 0 ≈ 0 . 3 9 2 7 has been marked correct.
In future, if you spot any errors with a problem, you can “report” it by selecting "report problem" in the “line line line” menu in the top right corner. This will notify the problem creator who can fix the issues.
Oh really sorry. I was unknown about angle unit.
I will remember this thing.
I solved it using trigonometry. From where did you get this solution?
Log in to reply
That's why i posted this solution. Everyone can solve it with trigonometry.
But the motto was to give "A pure geometric solution."
I designed it myself. Its my solution only.
Use the fact that the orthocenter and circumcenter are isogonal conjugates. This implies that the median of the triangle passes through the circumcenter of the triangle. Now, if the circumcenter does not lie on A B then this implies that either the triangle is isosceles (which is impossible since isosceles triangles have same median and angle bisector and altitude) or the triangle is degenerate. Since none of these cases can happen this must mean that the circumcenter is on A B which implies A B C is a right triangle. Let the foot of the altitude from C be D . Similarities tell us that ∠ D C B = ∠ C A B = 4 9 0 ∘ = 2 2 . 5 ∘ . Therefore, our answer is 2 2 . 5 ∘ .