Colourful Square

Let $x$ be the side of the square.

Red area: $R\sqrt{2}+R=x$ , then $R=x(\sqrt{2}-1)$ and $\color{#D61F06}{R_E=\pi x^2(\sqrt{2}-1)^2}$ .

Blue area: $r\sqrt{2}+r=x\sqrt{2}-x$ , then $r=x(\sqrt{2}-1)^2$ and $\color{#3D99F6}{B_L=\pi x^2(\sqrt{2}-1)^4}$

Brown area: $\color{#624F41}{B_R=x^2-\frac{\pi x^2}{4}-B_L}$ , then $\color{#624F41}{B_R=x^2\left(1-\frac{\pi}{4}\right)-B_L}$

Yellow area: $\color{#EC7300}{Y=R^2-\frac{\pi R^2}{4}=R^2\left(1-\frac{\pi}{4}\right)}$ , then $\color{#EC7300}{Y=x^2(\sqrt{2}-1)^2\left(1-\frac{\pi}{4}\right)}$ .

Green area: $\color{#20A900}{G=\frac{1}{2}\left(\frac{\pi x^2}{4}-R_E-Y\right)}$

Then we have $S=\dfrac{\pi x^2(\sqrt{2}-1)^4 x^2\left(1-\frac{\pi}{4}\right)}{\pi x^2(\sqrt{2}-1)^2 x^2(\sqrt{2}-1)^2\left(1-\frac{\pi}{4}\right)}+2\left(\frac{\pi x^2}{4}-R_E-Y\right)$

$S=1+2\left(\frac{\pi (\sqrt{2}+1)^2}{4}-\pi (\sqrt{2}+1)^2(\sqrt{2}-1)^2-(\sqrt{2}+1)^2(\sqrt{2}-1)^2\left(1-\frac{\pi}{4}\right)\right)$

$S=1+2\left(\frac{\pi (3+2\sqrt{2})}{4}-\pi-1+\frac{\pi}{4}\right)$

$S=1+2\left(\frac{3\pi}{4}+\frac{\pi\sqrt{2}}{2}-\pi-1+\frac{\pi}{4}\right)$

$S=1+\pi\sqrt{2}-2$

$S=\pi\sqrt{2}-1\approx \boxed{3.4429}$

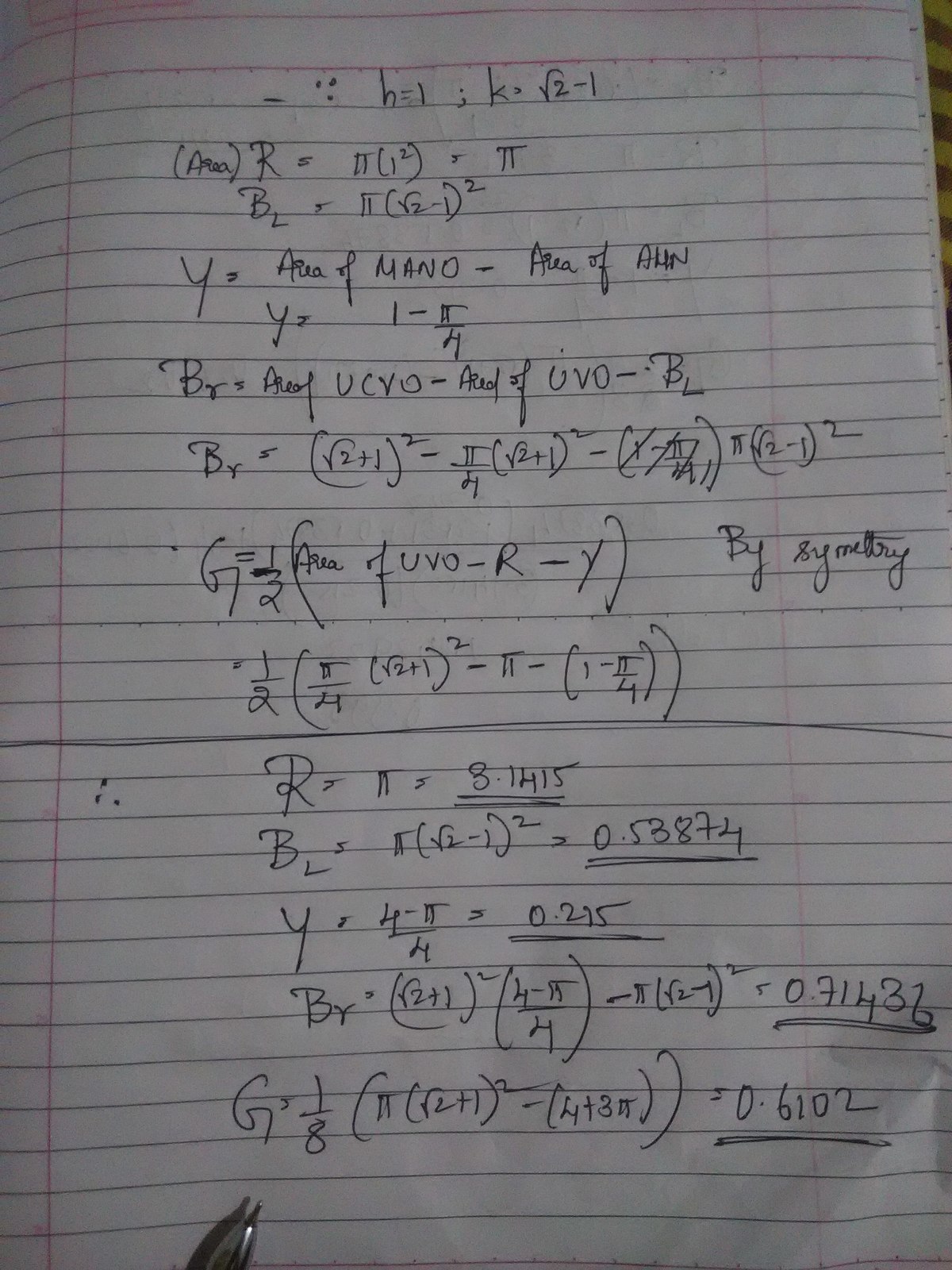
So on finding the given expression, you get the answer as $\color{#3D99F6}{\boxed{3.4403}}$ in my case. So the answer is within my calculation errors.

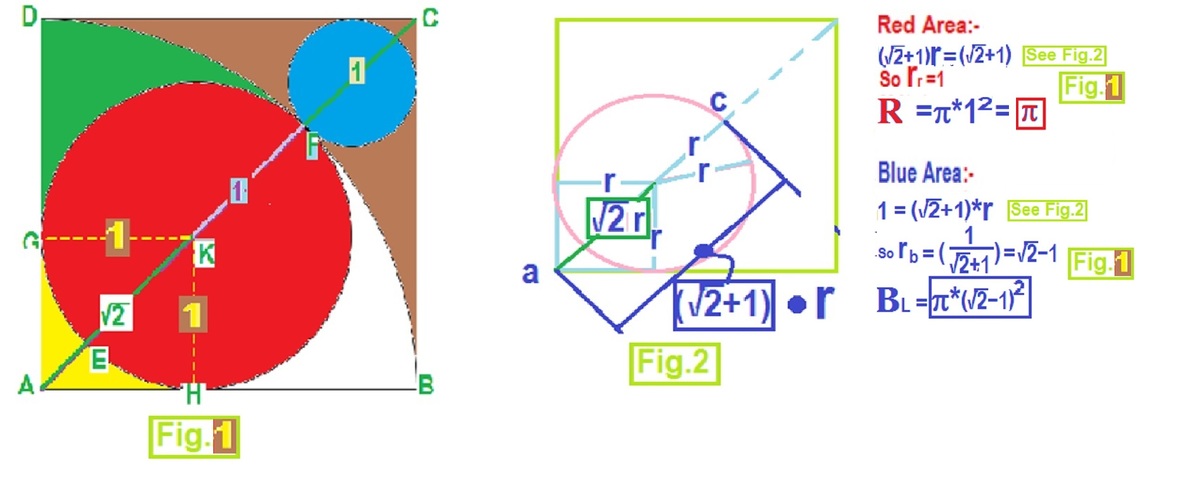
The problem is based on relation between a square and full or quarter circles within it, so that we can find certain areas. There are three types of relations in this problem.

AC, the diagonal of square ABCD, $( side =1+\sqrt2 )=\sqrt2*( 1+\sqrt2 )=2+\sqrt2.$

Fig. 2 shows how to find area of a circle tangent to the two adjoining sides of a square. There is the corner where the sides meet. The extended diameter of the circle meet the corner. The distance of the far end of the diameter from the corner = $(\sqrt2+1)*radius.$ . This diameter is along the square diagonal from the corner.
AF=radius of quarter circle=side of the square. It is along AC. For the red circle, AF is also the "corner far end" distance. So red radius is calculated as 1.
CF=AC - AF=1 is the "corner far end" distance for blue circle. So blue radius is calculated as (\sqrt2 - 1).

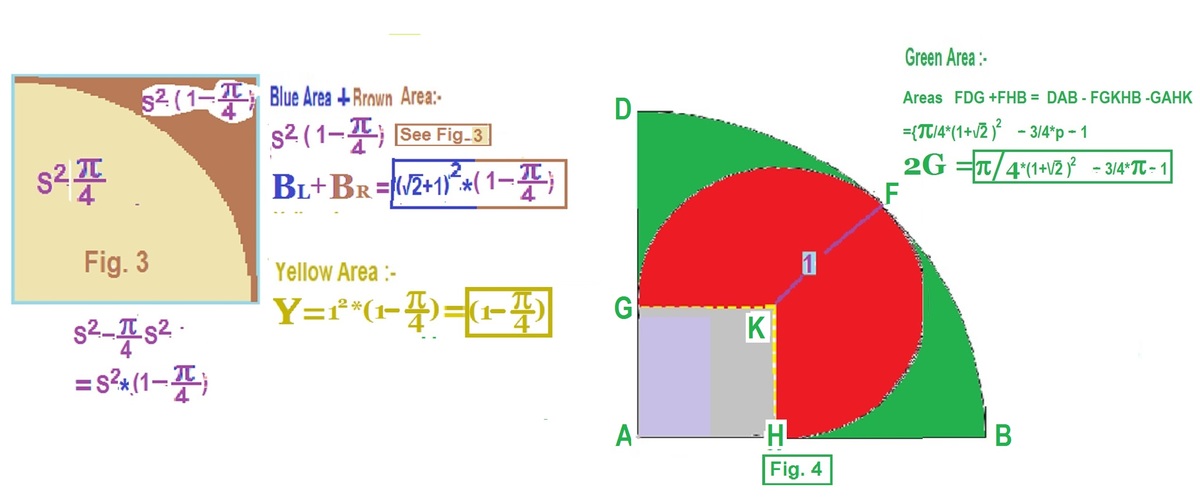
Fig. 3 shows how to find the area left after the quarter circle is taken away from the square. This area is $S^2 - \dfrac \pi 4*S^2=S^2*(1 - \frac \pi 4)$ Square area ABCD - quarter circle area EDAB =Brown area + Blue circle $=(1+\sqrt2)^2 *(1 - \frac \pi 4)$
Square area AHKG - one fourth red circle area GEHK = Yellow area $= 1^2*(1 - \frac \pi 4)$

Fig. 4 is a little complicated. How ever can be simplified as shown. Here it is areas FDAHG taken away from quarter circle. This is shown in the sketch itself. Note that taken white area also since it has the same area.

Taking the values from the sketch:-

\dfrac{\color{#3D99F6}{B_L}(\color{#624F41}{B_R}+\color{#3D99F6}{B_L})}{\color{#D61F06}{R}\color{#EC7300}{Y}} +4\color{#20A900}{G}\\ =\dfrac{\pi\!*\!(\sqrt2 - 1)^2\!*\!( \sqrt2\!+\!1)^2\!*\!(1 - \frac \pi 4)}{\pi*(1- \frac \pi 4)}+2* \{ \frac \pi 4*( \sqrt2\!+\!1)^2-\frac 3\! 4\! *\pi - 1 \}=\huge ~~~\color{#D61F06}{3.44288}.