Have you learnt Newton sum?
A polynomial 5 x 2 − 6 x − 2 = 0 has roots α and β . Then, find ( α 5 + α 1 0 + β 1 0 + β 5 ) .
The answer is 54.56.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
Good approach. Glad you decided against calculating P 6 , P 7 , P 8 , P 9 .
How did you directly calculated P 1 0 ?? Is there any formula or shortcut to such manupulation ?? Thank you .
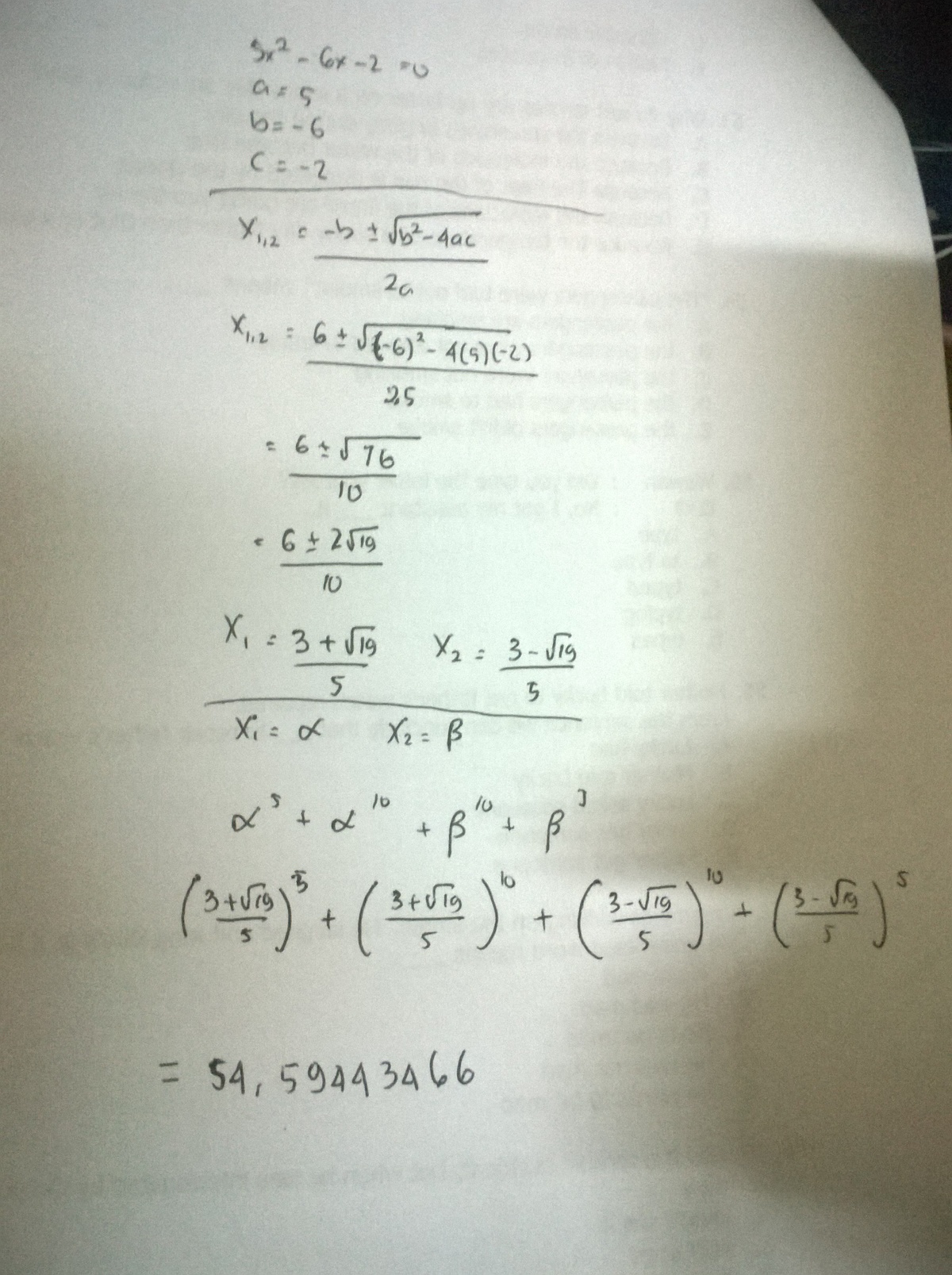
Vieta's Formula tells that α + β = 5 6 = e 1 and α β = − 5 2 = e 2 .
Now, P n = α n + β n can be computed using Newton's Identities for any positive integer n .
Using the calculations above we find that α 5 + α 1 0 + β 1 0 + β 5 = 5 1 0 5 3 3 1 4 8 7 7 6 = 5 4 . 5 9 4 4 3 4 6 6 2 4 .