Haven't you studied this in 1st grade?
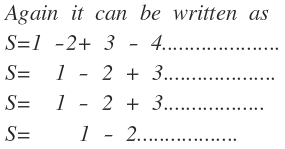Step 1: We define S= 1 -2+3-4...................
Step 2: See the photo above
Step 3: Adding the four Equations
Step 4: S = 1/4
That's nonsense, bu when I try to figure out where I was wrong I couldn't . Will you do that for me?
I will post the solutions tomorrow. Please visit to see that.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
All the operations which we learnt in First grade are valid only on convergent series. We can't simply add two divergent series even if they are same. In fact, we can't rearrange the terms also in divergent series. By rearrangement, I mean that in above series we can't rearrange the terms as S= (1+3+5+7...........) - (2+4+6+8...............). If we do so, we can get different answers for different arrangements.
What I have done that I rearranged the terms in sequence and then added them which is not allowed for divergent series.
What I meant when I said that we will get different answer for different arrangements:
In question, we have seen that answer is 1/4. Focus on the sequence given in solution above.
Sum of odd numbers upto n is n^2 and sum of even number upto n is n(n+1). If I substitute this value in above equation, I get
S=n^2 - n(n+1) = -n
As n is tending to infinity, I get the answer as -(infinity)
But, now the question arises, what's the exact value of S. We can't tell the exact value, But by carefully analysing the series, we see that each positive term is succeeded by a negative terms whose magnitude is greater than positive term, So the answer is -(infinity). Since, we can conclude nothing about infinity, we say that the series diverges over R.