He doesn't have a lead foot, it just looks that way
Since the speed of light is finite (equal to c = 3 × 1 0 8 ( m / s ) ), when we observe an object that is moving with constant speed, it can actually appear to have an acceleration. We'll call this an "apparent acceleration". As an example, consider a car moving on a straight road with a constant velocity v = 5 0 m / s . An observer stands a distance d = 5 m from the side of the road and watches the car. Find the maximum "apparent acceleration" in μ m / s 2 the observer sees as she watches the car approach her and then move away.
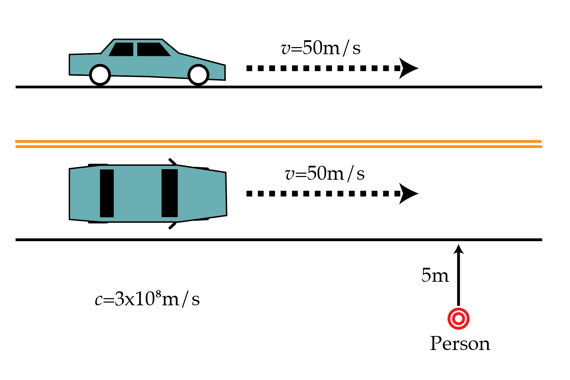
Hint: Can you figure out the position the observer believes the car is at at each instant in time?
Details and assumptions
- 1 ( μ m ) = 1 0 − 6 ( m )
The answer is 83.33.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Are you considering at time t=0 the apparent time at which the car is passing x=0? Otherwise I think there will be some additional terms owing to the discrete nature of light.
Mark origin at the perpendicular from the person to the road and axis along the road in the direction of motion of the car. The person is at a distance l from the road (instead of using d as in question so that there is no symbol confusion when doing calculus)
Suppose the person sees the car at position x ′ at time t . This would correspond to the car sending him light from x ′ at some previous time. At that time the distance between the car and the person would be h = x ′ 2 + l 2 . Light would have take Δ t = c h = c x ′ 2 + l 2 time to reach the person from there. So the current position of the car would be x = x ′ + v Δ t i.e. \begin{equation} x={x}'+\dfrac{v}{c}\sqrt{{x}'^2+l^2} \tag{1} \end{equation}
The "apparent acceleration" would be given by a ′ = d t 2 d 2 x ′ and "apparent velocity" would be given by v ′ = d t d x ′ . For this differentiate the equation ( 1 ) twice.
\begin{equation} v=\frac{dx}{dt}=\frac{d}{dt}\left( {x}'+\frac{v}{c}\sqrt{{{{{x}'}}^{2}}+{{l}^{2}}} \right) \end{equation} \begin{equation} v={v}'+\frac{v}{c}\frac{2{x}'{v}'}{2\sqrt{{{{{x}'}}^{2}}+{{l}^{2}}}} \end{equation} \begin{equation} v={v}'\left( 1+\frac{v}{c}\frac{{{x}'}}{\sqrt{{{{{x}'}}^{2}}+{{l}^{2}}}} \right) \tag{2} \end{equation}
Note that the real acceleration of car is 0 \begin{equation} a=\frac{dv}{dt}=0=\frac{d}{dt}\left( {v}'\left( 1+\frac{v}{c}\frac{{{x}'}}{\sqrt{{{{{x}'}}^{2}}+{{l}^{2}}}} \right) \right) \end{equation}
\begin{equation} 0={a}'\left( 1+\frac{v}{c}\frac{{{x}'}}{\sqrt{{{{{x}'}}^{2}}+{{l}^{2}}}} \right)+{v}'\frac{v}{c}\left( \frac{\sqrt{{{{{x}'}}^{2}}+{{l}^{2}}}\,{v}'-{x}'\frac{2{x}'{v}'}{2\sqrt{{{{{x}'}}^{2}}+{{l}^{2}}}}}{{{{{x}'}}^{2}}+{{l}^{2}}} \right) \end{equation}
\begin{equation} {a}'=-\frac{v{{{{v}'}}^{2}}{{l}^{2}}}{c\left( 1+\frac{v}{c}\frac{{{x}'}}{\sqrt{{{{{x}'}}^{2}}+{{l}^{2}}}} \right){{\left( {{{{x}'}}^{2}}+{{l}^{2}} \right)}^{\frac{3}{2}}}} \end{equation} The denominator terms increase as x ′ increases so maximum magnitude of acceleration occurs at x ′ = 0 and then v = v ′ from equation ( 2 ) and \begin{equation} {a}'=\frac{v{{{{v}'}}^{2}}{{l}^{2}}}{c{{\left( {{l}^{2}} \right)}^{\frac{3}{2}}}}=\frac{v{{{{v}'}}^{2}}}{cl}=\frac{v^3}{cl}=\frac{{{50}^{3}}}{3\times {{10}^{8}}\times 5}\frac{\text{m}}{\text{s}} \end{equation}
\begin{equation} {a}'=\frac{25000}{300}\frac{\mu\text{m}}{\text{s}}=\frac{250}{3}\frac{\mu\text{m}}{\text{s}}=83.33\frac{\mu\text{m}}{\text{s}} \end{equation}
Let's call the place where our the observer stands on "A", the closest point to A on the road "O", the real position of the car at a certain given time "X" and the observed position of the car at a certain given time "Y". Let x = O X , y = O Y , d = O A , and choose our time such that at t = 0 we have x = 0 and so x ( t ) = v t .
The observed position and the real position of the car is not the same due to the time lag that comes from the finite nature of the speed of light. The time lag Δ t is equal to both v x − y and c y 2 + d 2 . With these 2 equations and x = v t one can solve for y:
y = c 2 − v 2 v ( c 2 t − c 2 v 2 t 2 + d 2 ( c 2 − v 2 ) ) ⇒ d t 2 d 2 y = y ¨ = a y = − ( c 2 v 2 t 2 + d 2 ( c 2 − v 2 ) ) 3 / 2 v 3 c 2 d 2
The largest magnitude of the apparent acceleration is at t = 0 : ∣ a y ∣ m a x = ∣ a y ( t = 0 ) ∣ = d ( c 2 − v 2 ) 3 / 2 v 3 c 2 = 8 . 3 3 3 × 1 0 − 5 ( m / s 2 ) = 8 3 . 3 3 ( μ m / s 2 )
Let t = 0 and x = 0 when the car is at the position closest to the person. Suppose the car is travelling in the position x direction, then the car would be at position x at time t = 5 0 x . Light takes time to travel from the car to the observer, so to the observer the car would be at position x at the apparent time t = 5 0 x + c x 2 + 5 2 . Differentiate this equation with respect to t , and we get
1 = 5 0 1 x ˙ + c 1 x 2 + 5 2 x x ˙
⇒ x ˙ = ( 5 0 1 + c x 2 + 5 2 x ) − 1
Differentiating it again we get
0 = x ¨ ( 5 0 1 + c x 2 + 5 2 x ) + 2 5 c x ˙ 2 ( x 2 + 5 2 ) − 3 / 2
⇒ x ¨ = − c 2 5 ( 5 0 1 x 2 + 2 5 + c x ) − 3
Hence to find maximum acceleration (or rather, deceleration), we need to find the minimum value of 5 0 1 x 2 + 2 5 + c x = α
Rearranging the above equation and squaring both sides we can obtain
( 2 5 0 0 1 − c 2 1 ) x 2 + c 2 α x + 1 0 0 1 − α 2 = 0
And by using the fact that discriminant ≥ 0 and manipulating the equations, we can obtain
α 2 ≥ 1 0 0 1 − c 2 2 5
Hence,
maximum deceleration = c 2 5 α − 3 = c 2 5 ( 1 0 0 1 − c 2 2 5 ) − 3 / 2 = 8 3 . 3 × 1 0 − 6